another Cauchy peculiarity [aka the witch of Agnesi]
 Following a homework question on X validated, easily solved by a change of variables, I realised that the distribution of X/(X+Y) when X and Y are iid N(0,1) is again a Cauchy distribution but with both location and scale equal to ½! That the scale is ½ sort of makes sense due to the numerator being half (in distribution!) of the denominator, but the decentering of the distribution is more puzzling. And it does hold in the sense that
Following a homework question on X validated, easily solved by a change of variables, I realised that the distribution of X/(X+Y) when X and Y are iid N(0,1) is again a Cauchy distribution but with both location and scale equal to ½! That the scale is ½ sort of makes sense due to the numerator being half (in distribution!) of the denominator, but the decentering of the distribution is more puzzling. And it does hold in the sense that
> median(1/(1+rnorm(1e6)/rnorm(1e6))) [1] 0.4990263 > median(abs(.5-1/(1+rnorm(1e6)/rnorm(1e6)))) [1] 0.5014334
With the even more amazing
> mean(1/(1+rnorm(1e6)/rnorm(1e6))) [1] 0.4796456
Well (spoiler!) the last result was actually cherry-picked out of two dozens attempts as the closest to .5! With the other values wildly variable… Another answer by W. Huber gives the intuition behind the ½ since
x/(x+y) = ½ + ½ (x-y)/(x+y)
Cauchy being a local (in the sense that he is buried in Sceaux!, in the same cemetery as Galois whose research he supported despite being usually accused of having rejected his papers), with a rather nasty reputation!, and as I had had a drink with Steve Stigler the day before, I looked around for the true originator of Cauchy’s distribution, who is Simeon Poisson, true to Stigler’s eponym law!, who used it as a counter-example to the Law of Large Numbers. Later, Cauchy used the distribution (without acknowledging Poisson) as a counter example in a dispute with Bienaymé on the most probable nature of the least square estimator. The name of “witch of Agnesi” is pointed out in Steve’s 1974 Biometrika paper, making reference to the mathematician Maria Agnesi (1718-1799) who used the denomination, unrelated with the weird statistical properties of the “Cauchy” distribution.
December 6, 2019 at 6:09 pm
Il te faut savoir que si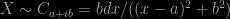 alors pour toute homographie
alors pour toute homographie  croissante la loi de
croissante la loi de 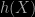 est $C(h(a+ib))$. Plus de details dans ‘which functions preserve Cauchy laws’ Proceedings of the American Mathematical Society dans les annees 1986 ou 7.
est $C(h(a+ib))$. Plus de details dans ‘which functions preserve Cauchy laws’ Proceedings of the American Mathematical Society dans les annees 1986 ou 7.
December 6, 2019 at 6:57 pm
Merci Gérard! Et meilleurs voeux.