MCMC on zero measure sets

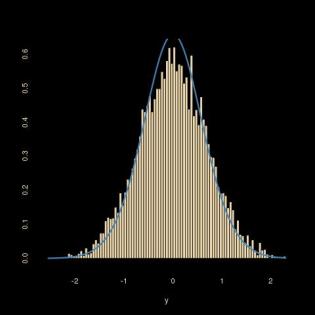Simulating a bivariate normal under the constraint (or conditional to the fact) that x²-y²=1 (a non-linear zero measure curve in the 2-dimensional Euclidean space) is not that easy: if running a random walk along that curve (by running a random walk on y and deducing x as x²=y²+1 and accepting with a Metropolis-Hastings ratio based on the bivariate normal density), the outcome differs from the target predicted by a change of variable and the proper derivation of the conditional. The above graph resulting from the R code below illustrates the discrepancy!

targ=function(y){
  exp(-y^2)/(1.52*sqrt(1+y^2))}

T=10^5
Eps=3
ys=xs=rep(runif(1),T)
xs[1]=sqrt(1+ys[1]^2)
for (t in 2:T){
  propy=runif(1,-Eps,Eps)+ys[t-1]
  propx=sqrt(1+propy^2)
  ace=(runif(1)<(dnorm(propy)*dnorm(propx))/
               (dnorm(ys[t-1])*dnorm(xs[t-1])))
  if (ace){
     ys[t]=propy;xs[t]=propx
     }else{
       ys[t]=ys[t-1];xs[t]=xs[t-1]}}

If instead we add the proper Jacobian as in

  ace=(runif(1)<(dnorm(propy)*dnorm(propx)/propx)/
               (dnorm(ys[t-1])*dnorm(xs[t-1])/xs[t-1]))

the fit is there. My open question is how to make this derivation generic, i.e. without requiring the (dreaded) computation of the (dreadful) Jacobian.