gap frequencies [& e]

A riddle from The Riddler where brute-force simulation does not pay:

For a given integer N, pick at random without replacement integers between 1 and N by prohibiting consecutive integers until all possible entries are exhausted. What is the frequency of selected integers as N grows to infinity?

A simple implementation of the random experiment is as follows

generope=function(N){
  frei=rep(1,N)
  hus=0
  while (max(frei)==1){
    i=sample(rep((1:N)[frei==1],2),1)
    frei[i]=frei[i+1]=frei[i-1]=0
    hus=hus+1}
  return(hus)}

It is however quite slow and does not exploit the recursive feature of the sampling, namely that the first draw breaks the set {1,…,N} into two sets:

generipe=function(N){
  if (N<2){ return((N>0))}else{
   i=sample(1:N,1)
   return(1+generipe(i-2)+generipe(N-i-1))}}

But even this faster solution takes a while to run for large values of N:

frqns=function(N){
  space=0
  for (t in 1:1e3) space=space+generipe(N)
  return(space/(N*1e3))}

as for instance

>  microbenchmark(frqns(100),time=10)
Unit: nanoseconds
       expr       min        lq         mean    median        uq       max
 frqns(100) 178720117 185020903 212212355.77 188710872 205865816 471395620
       time         4         8        26.13        32        37       102

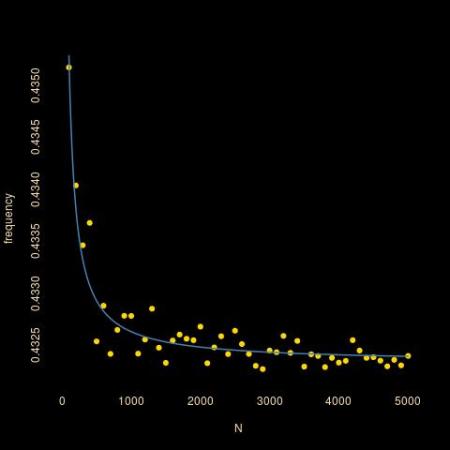
Hence this limits the realisation of simulation to, say, N=10⁴. Thinking further about the recursive aspect of the process however leads to a recursion on the frequencies q_N, as it is straightforward to prove that

with q₁=1 and q₂=1/2. This recursion can be further simplified into

which allows for a much faster computation

s=seq(1,1e7) #s[n]=n*q[n]
for (n in 3:1e7) s[n]=(1+2*s[n-2]+(n-1)*s[n-1])/n

and a limiting value of 0.4323324… Since storing s does not matter, a sliding update works even better:

a=b=1
for (n in 3:1e8){ c=(1+2*a+(n-1)*b)/n;a=b;b=c}

still producing a final value of 0.4323324, which may mean we have reached some limit in the precision.

As I could not figure out a way to find the limit of the sequence (1) above, I put it on the maths forum of Stack Exchange and very quickly got the answer (obtained by a power series representation) that the limit is (rather amazingly!)

which is 0.432332358.., hence very close to the numerical value obtained for n=3×10⁸. (Which does not change from n=10⁸, once again for precision reasons.) Now I wonder whether or not an easier derivation of the above is feasible, but we should learn about it in a few hours on The Riddler. [Update: The solution published by The Riddler is exactly that one, using a power series expansion to figure out the limit of the series, unfortunately. I was hoping for a de Montmort trick or sort of…]