Hamiltonian MC on discrete spaces [a reply from the authors]
 Q. Why not embed discrete parameters so that the resulting surrogate density function is smooth?
Q. Why not embed discrete parameters so that the resulting surrogate density function is smooth?
A. This is only possible in very special settings. Let’s say we have a target distribution π(θ, n), where θ is continuous and ‘n’ is discrete. To construct a surrogate smooth density, we would need to somehow smoothly interpolate a collection of functions fn(θ) = π(θ, n) for n = 1, 2, …. It is not clear to us how we can achieve this in a general and tractable way.
Q. How to generalize the algorithm to a more complex parameter space?
A. We provide a clear solution to dealing with a discontinuous target density defined on a continuous parameter space. We agree, however, that there remains the question of whether and how a more complex parameter space can be embedded into a continuous space. This certainly deserves a further investigation. For example, a binary tree can be embedded in to an interval [0,1] through a dyadic expansion of a real number.
Q. Physical intuition of discontinuous Hamiltonian dynamics is not clear from a theory of differential measure-valued equation and selection principle.
A. Hamiltonian dynamics with a discontinuous potential energy has long been used by physicists as a natural model for some physical phenomena (also known as “impulsive systems”). The main difference from a smooth system is that a gradient become a “delta function” at the discontinuity, causing an instantaneous “push” toward the direction of lower potential energy. A theory of differential measure-valued equation / inclusion and selection principle is only a mathematical formalization of such physical systems.
Q. (A special case of) DHMC looks like taking multiple Gibbs steps?
A. The crucial difference from Metropolis-within-Gibbs is the presence of momentum in DHMC, which helps guide a Markov chain toward a high density region.
The effect of momentum is evident in the Jolly-Seber example of Section 5.1, where DHMC shows 60-fold efficiency improvement over a sampler “NUTS-Gibbs” based on conditional updates. Also, a direct comparison of DHMC and Metropolis-within-Gibbs can be found in Section S4.1 where DHMC, thanks to the momentum, is about 7 times more efficient than Metropolis-within-Gibbs (with optimal proposal variances).
Q. Unlike HMC, DHMC does not seem to use structural information about the parameter space and local information about the target density?
A. It does. After all, other than the use of Laplace momentum and discontinuity in the target density, DHMC is based on the same principle as HMC — simulating Hamiltonian dynamics to generate a proposal.
The confusion is perhaps due to the fact that the coordinate-wise integrator of DHMC does not require gradients. The gradient of the log density — which may be a “delta” function at discontinuities — plays a clear role if you look at Hamilton’s equations Eq (10) corresponding to a Laplace momentum. It’s just that, thanks to a property of a Laplace momentum and conservation of energy principle, we can approximate the exact dynamics without ever computing the gradient. This is in fact a remarkable property of a Laplace momentum and our coordinate-wise integrator.
July 9, 2017 at 6:48 pm
“A. Hamiltonian dynamics with a discontinuous potential energy has long been used by physicists as a natural model for some physical phenomena (also known as “impulsive systems”). The main difference from a smooth system is that a gradient become a “delta function” at the discontinuity, causing an instantaneous “push” toward the direction of lower potential energy. A theory of differential measure-valued equation / inclusion and selection principle is only a mathematical formalization of such physical systems.”
My standard mathematical scepticism (that generalisations of true results can’t be assumed to be true) really can’t get past this. Are there references that Hamiltonian systems with discontinuous Hamiltonian behave exactly like ordinary systems? Because as far as I could see, none of your references talked about that. The closes was the “health warning” in section 4.2 of Strewart, which basically said “be careful with your numerics”.
So my mathematical questions are:
1) what, in any, ways are the continuous dynamics different from those of a standard Hamiltonian system
2) does the numerical scheme converge. If so, what notion of a solution does it converge to.
Remembering that time Girolami and Calderhead missed a 1/2 in there RHMALA equations, these mathematical details make big differences!
July 17, 2017 at 4:15 pm
Thank you for the questions, Dan.
To rephrase (and to correct a typo (?)), the questions are:
Q1. In what ways is discontinuous Hamiltonian dynamics different from smooth one?
Q2. Does the numerical scheme converge? If so, in what sense?
Just a note to begin with: the second question relates to the acceptance rate of discontinuous HMC (DHMC) proposals as a function of stepsize . This is important for practical performances of DHMC, and we are in fact working on updating our arXiv draft with a theoretical analysis on it. We will post a new version hopefully within a few weeks.
. This is important for practical performances of DHMC, and we are in fact working on updating our arXiv draft with a theoretical analysis on it. We will post a new version hopefully within a few weeks.
Answer to Q1:
Practically speaking, the most important difference is numerical methods used to approximate the exact solution (as Dan correctly identified and as discussed further below). It is in general much more difficult and computationally intensive to accurately approximate discontinuous dynamics. This is exactly what lead us to propose Laplace momentum and the coordinate-wise integrator instead of dealing with Gaussian momentum.
On theoretical sides, mathematical analysis is much more challenging. For example, a proof of symplecticity has been done only in case-by-case manner to our knowledge (e.g. Theorem 3 in the paper and the elastic collision problem in Fetecau (2003)). Reversibility and energy preservation though is automatic in our definition of discontinuous Hamiltonian dynamics for piecewise smooth potential energy.
At qualitative levels, we do not find particularly important differences from smooth Hamiltonian dynamics. Discontinuous dynamics satisfies time reversibility, energy preservation, volume preservation, and is characterized as a limit of smooth dynamics. (What else do you need?) Of course, a particular choice of kinetic energy can have a significant impact on the corresponding Hamiltonian dynamics’ ability to explore the parameter space efficiently (whether or not the target is smooth). The properties of Laplace momentum based dynamics certainly deserves further theoretical and empirical investigations.
Answer to Q2: as
as 
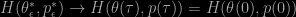 as
as 
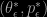 is the approximate solution based on
is the approximate solution based on  steps of the integrator. The rate of convergence in Hamiltonian is particularly important as the error in Hamiltonian directly relates to the acceptance probability of a proposal.
steps of the integrator. The rate of convergence in Hamiltonian is particularly important as the error in Hamiltonian directly relates to the acceptance probability of a proposal.
As mentioned above, the difference from smooth dynamics is most apparent in numerical methods and their properties. In particular, for discontinuous cases, it is important to distinguish two notions of convergences:
1. (strong convergence)
2. (convergence in Hamiltonian)
where
Let’s first discuss convergence in Hamiltonian. If we use only Laplace momentum (without mixing it with Gaussian) and the coordinate-wise integrator, then there the Hamiltonian is exactly preserved and the convergence occurs for any . (This is not to say that
. (This is not to say that  can be taken arbitrarily large; see Section 4.3.) When we use Gaussian momentum for continuous variables
can be taken arbitrarily large; see Section 4.3.) When we use Gaussian momentum for continuous variables 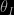 , then the error is
, then the error is  where
where 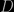 is the number of discontinuities along the exact trajectory for
is the number of discontinuities along the exact trajectory for ![t \in [0, \tau]](https://s0.wp.com/latex.php?latex=t+%5Cin+%5B0%2C+%5Ctau%5D&bg=000000&fg=B0B0B0&s=0&c=20201002) . This error is the same order as when the leapfrog is used for smooth dynamics and the constant factor in the error can be small when
. This error is the same order as when the leapfrog is used for smooth dynamics and the constant factor in the error can be small when  does not change dramatically for a small change in the discontinuous parameter
does not change dramatically for a small change in the discontinuous parameter 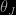 . The main idea behind the error analysis is that the local error (from one numerical integration step) is
. The main idea behind the error analysis is that the local error (from one numerical integration step) is  when no discontinuity is encountered and
when no discontinuity is encountered and  when a discontinuity is encountered. We empirically confirmed the
when a discontinuity is encountered. We empirically confirmed the  error rate in the Jolly-Seber example.
error rate in the Jolly-Seber example.
Quantifying the rate of strong convergence is trickier. With our coordinate-wise update approach, the velocity of an approximate trajectory is updated only one coordinate at a time. Because of this, when encountering a discontinuity, the approximate trajectory may get reflected (through a momentum flip ) along one coordinate or another depending on how exactly it approaches a discontinuity. Furthermore, the order of coordinate updates are randomized for reversibility, so this also affects the direction to which the trajectory gets reflected off. (Btw, this randomness in the direction of “bounce” is analogous to that of generalized bouncy particle sampler.) In a sense, the exact direction does not matter much since the trajectory gets reflected off toward a “right” direction in any case — toward a region of higher target density — and the convergence in Hamiltonian guarantees high acceptance rate.
) along one coordinate or another depending on how exactly it approaches a discontinuity. Furthermore, the order of coordinate updates are randomized for reversibility, so this also affects the direction to which the trajectory gets reflected off. (Btw, this randomness in the direction of “bounce” is analogous to that of generalized bouncy particle sampler.) In a sense, the exact direction does not matter much since the trajectory gets reflected off toward a “right” direction in any case — toward a region of higher target density — and the convergence in Hamiltonian guarantees high acceptance rate.
If one were to still insist on strong convergence, then we believe that the following result is true. If the discotinuity sets are only of the form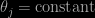 , then the absolute error is
, then the absolute error is  where
where  is the number of change in the signs of
is the number of change in the signs of  ‘s (and hence
‘s (and hence  ‘s) along the exact trajectory. (The assumption on the discontinuity set holds true for discrete parameters embedded into a continuous space.) Once
‘s) along the exact trajectory. (The assumption on the discontinuity set holds true for discrete parameters embedded into a continuous space.) Once  is small enough, the only source of error is the momentum flip move
is small enough, the only source of error is the momentum flip move  which qualitatively — but not precisely — approximate the behavior of the exact trajectory, and this is why the error is proportional to
which qualitatively — but not precisely — approximate the behavior of the exact trajectory, and this is why the error is proportional to  . In case of more complex boundaries, we are not sure if strong convergence is true due to the uncertainty in the direction to which the approximate trajectory gets reflected at discontinuities.
. In case of more complex boundaries, we are not sure if strong convergence is true due to the uncertainty in the direction to which the approximate trajectory gets reflected at discontinuities.