Naturally amazed at non-identifiability
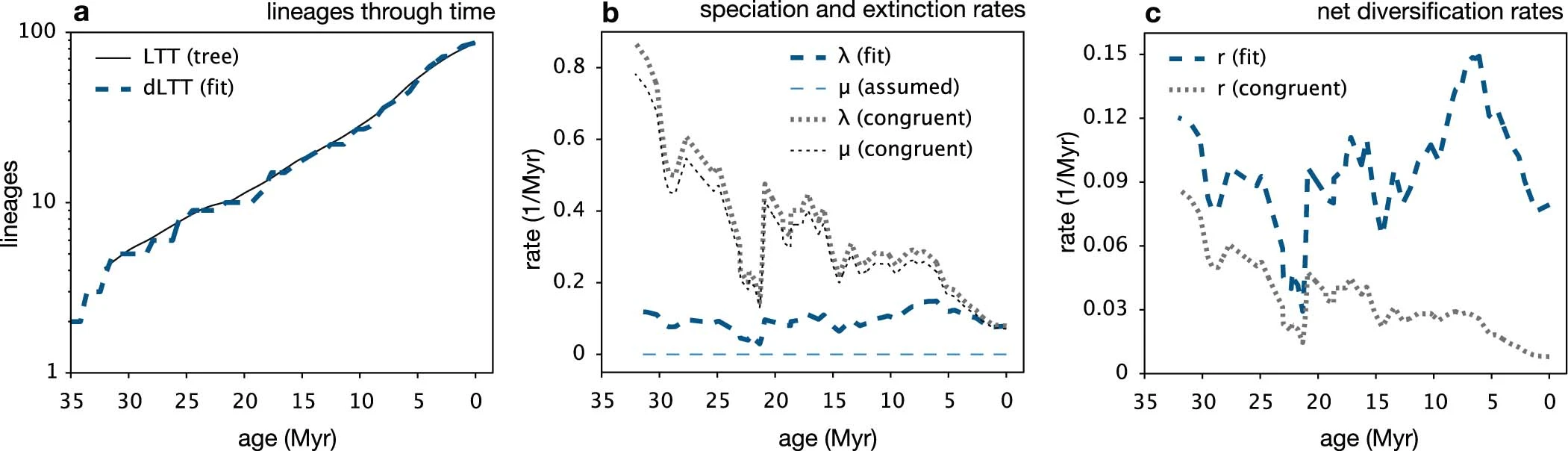 A Nature paper by Stilianos Louca and Matthew W. Pennell, Extant time trees are consistent with a myriad of diversification histories, comes to the extraordinary conclusion that birth-&-death evolutionary models cannot distinguish between several scenarios given the available data! Namely, stem ages and daughter lineage ages cannot identify the speciation rate function λ(.), the extinction rate function μ(.) and the sampling fraction ρ inherently defining the deterministic ODE leading to the number of species predicted at any point τ in time, N(τ). The Nature paper does not seem to make a point beyond the obvious and I am rather perplexed at why it got published [and even highlighted]. A while ago, under the leadership of Steve, PNAS decided to include statistician reviewers for papers relying on statistical arguments. It could time for Nature to move there as well.
A Nature paper by Stilianos Louca and Matthew W. Pennell, Extant time trees are consistent with a myriad of diversification histories, comes to the extraordinary conclusion that birth-&-death evolutionary models cannot distinguish between several scenarios given the available data! Namely, stem ages and daughter lineage ages cannot identify the speciation rate function λ(.), the extinction rate function μ(.) and the sampling fraction ρ inherently defining the deterministic ODE leading to the number of species predicted at any point τ in time, N(τ). The Nature paper does not seem to make a point beyond the obvious and I am rather perplexed at why it got published [and even highlighted]. A while ago, under the leadership of Steve, PNAS decided to include statistician reviewers for papers relying on statistical arguments. It could time for Nature to move there as well.
“We thus conclude that two birth-death models are congruent if and only if they have the same rp and the same λp at some time point in the present or past.” [S.1.1, p.4]
Or, stated otherwise, that a tree structured dataset made of branch lengths are not enough to identify two functions that parameterise the model. The likelihood looks like
$
where E(.) is the probability to survive to the present and ψ(s,t) the probability to survive and be sampled between times s and t. Sort of. Both functions depending on functions λ(.) and μ(.). (When the stem age is unknown, the likelihood changes a wee bit, but with no changes in the qualitative conclusions. Another way to write this likelihood is in term of the speciation rate λp
where Λp is the integrated rate, but which shares the same characteristic of being unable to identify the functions λ(.) and μ(.). While this sounds quite obvious the paper (or rather the supplementary material) goes into fairly extensive mode, including “abstract” algebra to define congruence.
“…we explain why model selection methods based on parsimony or “Occam’s razor”, such as the Akaike Information Criterion and the Bayesian Information Criterion that penalize excessive parameters, generally cannot resolve the identifiability issue…” [S.2, p15]
As illustrated by the above quote, the supplementary material also includes a section about statistical model selections techniques failing to capture the issue, section that seems superfluous or even absurd once the fact that the likelihood is constant across a congruence class has been stated.
November 24, 2020 at 4:51 pm
This paper was super complicated to read and doesn’t seem that the results are being right discussed, could you give a simple explanation why this paper is so wrong?
While it has so many citations until now?
November 25, 2020 at 7:55 am
I have somehow forgotten all about it!