Exchange algorithm

Following a comment by Mark Johnson on the ABC lectures, I read Murray, Ghahramani and MacKay’s “Doubly-intractable distributions” paper. As I already wrote in a reply to this comment,

The link to the paper is quite relevant. First, because those doubly untractable distributions are a perfect setting for ABC. Second, because the solution of Moller, Pettit, Berthelsen and Reeves (2004, Biometrika) is a close alternative to ABC. Indeed, the core of the Moller et al.’ method is to simulate pseudo-data as in ABC, in order to cancel the untractable part of the likelihood. If one uses as target density on the auxiliary pseudo-data the indicator function used in ABC (assuming this results in a density on the pseudo-data), then we get rather close to ABC-MCMC! Of course, there still are differences in that
(a) the auxiliary variable method of Moller et al. (2004) and Murray et al. (2006) still requires (the functional) part of the likelihood function to be available;
(b) the A in ABC-MCMC approach stands for approximative;
(c) the connection only works when considering a distance between the data and the pseudo-data, not when using summary statistics.
It would nonetheless be interesting to see a comparison between both approaches, for instance in a Potts model.

To be more precise, equation (9) in Murray et al. (2006)  is very similar to ABC if 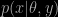is replaced by the indicator function of the proximity to y (assuming a uniform distribution is available). In that case (9) becomes

I also found the exchange algorithm interesting because it uses a straightforward importance sampling estimator of the normalising constant ratio,

leading to the acceptance probability

not the least because this leads to an unbiased estimator of the Metropolis-Hastings acceptance probability in the spirit of Andrieu and Roberts (2009, Annals of Statistics).