parallelizing MCMC with random partition trees
 Another arXived paper in the recent series about big or tall data and how to deal with it by MCMC. Which pertains to the embarrassingly parallel category. As in the previously discussed paper, the authors (Xiangyu Wang, Fangjian Guo, Katherine Heller, and David Dunson) chose to break the prior itself into m bits… (An additional point from last week criticism is that, were an unbiased estimator of each term in the product available in an independent manner, the product of the estimators would be the estimator of the product.) In this approach, the kernel estimator of Neiswanger et al. is replaced with a random partition tree histogram. Which uses the same block partition across all terms in the product representation of the posterior. And hence ends up with a smaller number of terms in the approximation, since it does not explode with m. (They could have used Mondrian forests as well! However I think their quantification of the regular kernel method cost as an O(Tm) approach does not account for Neiswanger et al.’s trick in exploiting the product of kernels…) The so-called tree estimate can be turned into a random forest by repeating the procedure several times and averaging. The simulation comparison runs in favour of the current method when compared with other consensus or non-parametric methods. Except in the final graph (Figure 5) which shows several methods achieving the same prediction accuracy against running time.
Another arXived paper in the recent series about big or tall data and how to deal with it by MCMC. Which pertains to the embarrassingly parallel category. As in the previously discussed paper, the authors (Xiangyu Wang, Fangjian Guo, Katherine Heller, and David Dunson) chose to break the prior itself into m bits… (An additional point from last week criticism is that, were an unbiased estimator of each term in the product available in an independent manner, the product of the estimators would be the estimator of the product.) In this approach, the kernel estimator of Neiswanger et al. is replaced with a random partition tree histogram. Which uses the same block partition across all terms in the product representation of the posterior. And hence ends up with a smaller number of terms in the approximation, since it does not explode with m. (They could have used Mondrian forests as well! However I think their quantification of the regular kernel method cost as an O(Tm) approach does not account for Neiswanger et al.’s trick in exploiting the product of kernels…) The so-called tree estimate can be turned into a random forest by repeating the procedure several times and averaging. The simulation comparison runs in favour of the current method when compared with other consensus or non-parametric methods. Except in the final graph (Figure 5) which shows several methods achieving the same prediction accuracy against running time.
Related
This entry was posted on July 7, 2015 at 12:15 am and is filed under Books, pictures, Statistics, University life with tags big data, embarassingly parallel, huge data, MCMC, Mondrian forests, parallel MCMC, random partition trees, tall data. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.
One Response to “parallelizing MCMC with random partition trees”
Leave a comment Cancel reply
This site uses Akismet to reduce spam. Learn how your comment data is processed.
July 7, 2015 at 6:05 am
Thanks for the review : ) Regarding Neiswanger et al, in the paper we are actually not criticizing on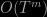 , but rather on
, but rather on  . Using their “one-at-a-time” trick, Neiswanger et al. reduce sampling complexity from
. Using their “one-at-a-time” trick, Neiswanger et al. reduce sampling complexity from 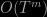 to
to  . However, even for
. However, even for  , when
, when 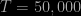 , the proposed independent Metropolis sampler still fails (The two toy examples). The reason is that an “independent” Metropolis sampler is extremely inefficient for a space containing
, the proposed independent Metropolis sampler still fails (The two toy examples). The reason is that an “independent” Metropolis sampler is extremely inefficient for a space containing  components (with different weights). Such failure indicates that we need to further reduce the sampling complexity from
components (with different weights). Such failure indicates that we need to further reduce the sampling complexity from  to
to  , which is the motivation for the paper. (Another motivation is the multi-scaleness)
, which is the motivation for the paper. (Another motivation is the multi-scaleness)