importance sampling with infinite variance
“In this article it is shown that in a fairly general setting, a sample of size approximately exp(D(μ|ν)) is necessary and sufficient for accurate estimation by importance sampling.”
Sourav Chatterjee and Persi Diaconis arXived yesterday an exciting paper where they study the proper sample size in an importance sampling setting with no variance. That’s right, with no variance. They give as a starting toy example the use of an Exp(1) proposal for an Exp(1/2) target, where the importance ratio exp(x/2)/2 has no ξ order moment (for ξ≥2). So the infinity in the variance is somehow borderline in this example, which may explain why the estimator could be considered to “work”. However, I disagree with the statement “that a sample size a few thousand suffices” for the estimator of the mean to be close to the true value, that is, 2. For instance, the picture I drew above is the superposition of 250 sequences of importance sampling estimators across 10⁵ iterations: several sequences show huge jumps, even for a large number of iterations, which are characteristic of infinite variance estimates. Thus, while the expected distance to the true value can be closely evaluated via the Kullback-Leibler divergence between the target and the proposal (which by the way is infinite when using a Normal as proposal and a Cauchy as target), there are realisations of the simulation path that can remain far from the true value and this for an arbitrary number of simulations. (I even wonder if, for a given simulation path, waiting long enough should not lead to those unbounded jumps.) The first result is frequentist, while the second is conditional, i.e., can occur for the single path we have just simulated… As I taught in class this very morning, I thus remain wary about using an infinite variance estimator. (And not only in connection with the harmonic mean quagmire. As shown below by the more extreme case of simulating an Exp(1) proposal for an Exp(1/10) target, where the mean is completely outside the range of estimates.) Wary, then, even though I find the enclosed result about the existence of a cut-off sample size associated with this L¹ measure quite astounding.![100 paths of importance sampling estimators using Exp(1) as proposal and Exp(10) as target, when estimating E[X]=10 exp10exp](https://xianblog.files.wordpress.com/2015/11/exp10exp.jpg?w=450&h=450)
“…the traditional approach of testing for convergence using the estimated variance of the importance sampling estimate has a flaw: for any given tolerance level ε, there is high probability that the test declares convergence at or before a sample size that depends only on ε and not on the two distributions f and g. This is absurd, since convergence may take arbitrarily long, depending on the problem”
The second part of the paper starts from the remark that the empirical variance estimate is a poor choice of convergence criterion. Especially when the theoretical variance does not exist. As put by Art Owen in his importance sampling notes, “Badly skewed weights could give a badly estimated mean along with a bad variance estimate that masks the problem”. The authors suggest to consider instead a sort of inverse effective sample size derived from the importance weights and given by max ω[t] / ∑ ω[t], which should be small enough. However, replicating the above Exp(1) versus Exp(1/10) example, the (selected) picture below shows that this criterion may signal that all is fine just before storm hits!
 The effective sample size has exactly the same issue in that a much lower value of the criterion may just be lurking around the corner. Which makes it hard to trust it at face value.
The effective sample size has exactly the same issue in that a much lower value of the criterion may just be lurking around the corner. Which makes it hard to trust it at face value.

May 13, 2017 at 6:35 pm
[…] Many thanks to Xian who first wondered about the occurence of these jumps. […]
May 13, 2017 at 6:34 pm
Your comment about the observed jumps made me wonder as well, so I wrote a small proof of the fact that they will appear infinitely often in the infinite variance case. You can find the note here: http://wp.me/p87SZW-LE. Thanks for sharing your insight!
May 13, 2017 at 7:08 pm
Merci, Olivier. Good point!
November 14, 2015 at 10:42 pm
This paper opens up an exciting fresh look at importance sampling. We might be able to control L1 error or even probability of an error exceeding a tolerable size, and dodge the issue of working with variances.
It remains difficult to get practical bounds. For example, put epsilon = 0.025 in Theorem 1.2, so 2epsilon = .05 (for 95% confidence, not a high level in the Monte Carlo context). Then exp(t/8) must be at least 40 and n must be exp(t) x exp(L), or about 6.5e12 times the nominal sample size exp(L). Good results are ensured at n = exp(L+t) and bad ones at n = exp(L-t) but those sample sizes are far apart.
Also, the upper bound on the error measure in Theorems 1.1 and 1.2 is proportional to the L2 norm of the integrand under the nominal measure \nu. That could be large or even infinite in importance sampling problems.
November 16, 2015 at 10:45 am
Thank you, Art. This is indeed a new approach to Monte Carlo assessment. I do remain uncomfortable with the use of infinite variance estimators, though, as I cannot trust their outcome.
November 13, 2015 at 12:05 pm
Thanks for the reference, Jonathan. Sorry I missed your 1503 paper (or maybe I got scared by the length!)
November 13, 2015 at 2:57 am
Thanks for the insightful post Christian. I wanted to point out an interesting connection. Dan Roy and I recently proposed using the same quantity Sourav and Persi introduced (in its ESS form) in the context of SMC with adaptive resampling (http://arxiv.org/pdf/1503.00966.pdf). In particular, we show that if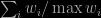 is used to measure effective sample size and is kept above
is used to measure effective sample size and is kept above  , where N is the number of particles, we obtain a
, where N is the number of particles, we obtain a  convergence rate for the KL divergence between true measure and the expected value of the SMC approximation.
convergence rate for the KL divergence between true measure and the expected value of the SMC approximation.
November 13, 2015 at 5:55 pm
As a coincidence goes: I went to the coffee room at CREST this afternoon for the first time in months and found your poster on this very paper posted there!