contemporary issues in hypothesis testing
This week [at Warwick], among other things, I attended the CRiSM workshop on hypothesis testing, giving the same talk as at ISBA last June. There was a most interesting and unusual talk by Nick Chater (from Warwick) about the psychological aspects of hypothesis testing, namely about the unnatural features of an hypothesis in everyday life, i.e., how far this formalism stands from human psychological functioning. Or what we know about it. And then my Warwick colleague Tom Nichols explained how his recent work on permutation tests for fMRIs, published in PNAS, testing hypotheses on what should be null if real data and getting a high rate of false positives, got the medical imaging community all up in arms due to over-simplified reports in the media questioning the validity of 15 years of research on fMRI and the related 40,000 papers! For instance, some of the headings questioned the entire research in the area. Or transformed a software bug missing the boundary effects into a major flaw. (See this podcast on Not So Standard Deviations for a thoughtful discussion on the issue.) One conclusion of this story is to be wary of assertions when submitting a hot story to journals with a substantial non-scientific readership! The afternoon talks were equally exciting, with Andrew explaining to us live from New York why he hates hypothesis testing and prefers model building. With the birthday model as an example. And David Draper gave an encompassing talk about the distinctions between inference and decision, proposing a Jaynes information criterion and illustrating it on Mendel‘s historical [and massaged!] pea dataset. The next morning, Jim Berger gave an overview on the frequentist properties of the Bayes factor, with in particular a novel [to me] upper bound on the Bayes factor associated with a p-value (Sellke, Bayarri and Berger, 2001)
B¹⁰(p) ≤ 1/-e p log p
with the specificity that B¹⁰(p) is not testing the original hypothesis [problem] but a substitute where the null is the hypothesis that p is uniformly distributed, versus a non-parametric alternative that p is more concentrated near zero. This reminded me of our PNAS paper on the impact of summary statistics upon Bayes factors. And of some forgotten reference studying Bayesian inference based solely on the p-value… It is too bad I had to rush back to Paris, as this made me miss the last talks of this fantastic workshop centred on maybe the most important aspect of statistics!
Xi'an's Og 
November 16, 2016 at 11:16 am
I have just read the Kamary et al. 2014 paper (arXiv:1412.2044) and agree that embedding the two models to be compared into one bigger model is a natural Bayesian solution. (It’s a pity you can’t give a philosophical reason for using arithmetic mixtures, but I can easily believe that the alternatives are “less practical to manage”).
November 16, 2016 at 11:22 am
Thank you for the support. I would also prefer using a geometric mixture to preserve the tail behaviour, but this is fraught with many difficulties.
November 13, 2016 at 7:48 pm
The inequality B¹⁰(p) ≤ 1/-e p log p can be obtained by maximizing the expression
over 
. But the advantage of the expression 
for a fixed 
is that it transforms p-values into Bayes factors, as Shafer et al. argue in their paper “Test Martingales, Bayes Factors and p-Values” (Statistical Science 26, 84-101, 2011, Section 6). Glenn Shafer used “Calibrate p-values by taking the square root” as the title of his talk at the Rutgers Foundations of Probability seminar in September. So one possibility is to replace a p-value p by the Bayes factor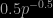 
. The advantage of this transformation is that it gives a Bayes factor, not an upper bound (and it’s more cautious).
November 14, 2016 at 12:00 pm
Actually the calibrator proposed by Glenn was even nicer: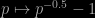
.
November 14, 2016 at 2:29 pm
Thank you for those precisions. Philosophically, I somewhat remain adverse to both p-values and Bayes factors, though!