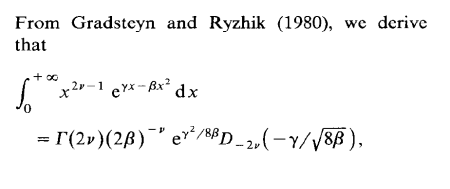I thought I did make a mistake but I was wrong…

One of my students in my MCMC course at ENSAE seems to specialise into spotting typos in the Monte Carlo Statistical Methods book as he found an issue in every problem he solved! He even went back to a 1991 paper of mine on Inverse Normal distributions, inspired from a discussion with an astronomer, Caroline Soubiran, and my two colleagues, Gilles Celeux and Jean Diebolt. The above derivation from the massive Gradsteyn and Ryzhik (which I discovered thanks to Mary Ellen Bock when arriving in Purdue) is indeed incorrect as the final term should be the square root of 2β rather than 8β. However, this typo does not impact the normalising constant of the density, K(α,μ,τ), unless I am further confused.

invariant conjugate analysis for exponential families

Here is a paper from Bayesian Analysis that I somehow missed and only become aware thanks to a (more) recent paper of the first author: in 2012, Pierre Druilhet and Denis Pommeret published invariant conjugate analysis for exponential families. The authors define a new class of conjugate families, called Jeffreys’ conjugate priors (JCP) by using Jeffreys’ prior as the reference density (rather than the uniform in regular conjugate families). Following from the earlier proposal of Druilhet and Marin (2007, BA). Both families of course coincide in the case of quadratic variance exponential families. The motivation for using those new conjugate priors is that the family is invariant by a change of parametrisation. And to include Jeffreys’ prior as a special case of conjugate prior. In the special case of the inverse Gaussian distribution, this approach leads to the conjugacy of the inverse normal distribution, a feature I noticed in 1991 when working on an astronomy project. There are two obvious drawbacks to those new conjugate families: one is that the priors are not longer always proper. The other one is that the computations associated with those new priors are more involved, which may explain why the authors propose the MAP as their default estimator. Since posterior expectations of the mean (in the natural representation [in x] of the exponential family) are no longer linear in x.

Harmonic means for reciprocal distributions

An interesting post on ExploringDataBlog on the properties of the distribution of 1/X. Hmm, maybe not the most enticing way of presenting it, since there does not seem anything special in a generic inversion! What attracted me to this post (via Rbloggers) is the fact that a picture shown there was one I had obtained about twenty years ago when looking for a particular conjugate prior in astronomy, a distribution I dubbed the inverse normal distribution (to distinguish it from the inverse Gaussian distribution).  The author, Ron Pearson [who manages to mix the first name and the second name of two arch-enemies of 20th Century statistics!] points out that well-behaved distributions usually lead to heavy tailed reciprocal distributions. Of course, the arithmetic mean of a variable X is the inverse of the harmonic mean of the inverse variable 1/X, so looking at those distributions makes sense. The post shows that, for the inverse normal distribution, depending on the value of the normal mean, the harmonic mean has tails that vary between a Cauchy and a normal distributions…