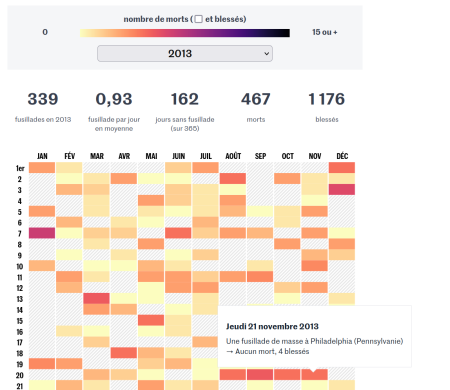
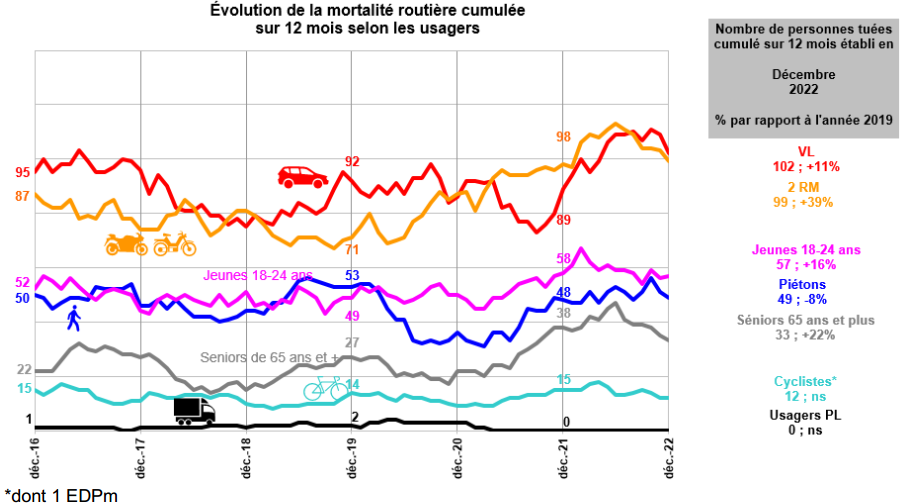
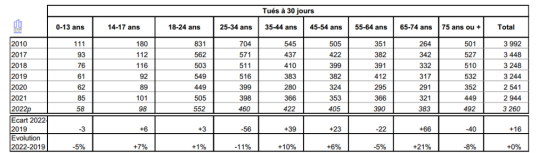
While running a “kitchen” workshop on Bayesian privacy in Les Houches, Le Monde published on π day a recap of a recent report on AI commanded by the French Government. Among other things, it contains recommendations on alleviating the administrative blocks in accessing personal data, based on a model for data protection created decades earlier around the CNIL structure. The final paragraph wishes for the creation of a “laboratory” that would test collaborative, altruistic, efficient models towards sharing data for learning, which is one of the main goals of OCEAN. Without mentioning any technical aspect, like an adoption of some privacy measure at a national or European level.