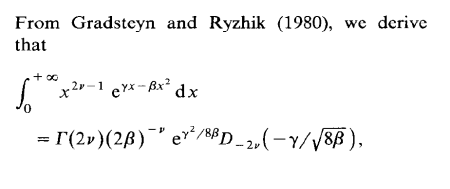I thought I did make a mistake but I was wrong…

One of my students in my MCMC course at ENSAE seems to specialise into spotting typos in the Monte Carlo Statistical Methods book as he found an issue in every problem he solved! He even went back to a 1991 paper of mine on Inverse Normal distributions, inspired from a discussion with an astronomer, Caroline Soubiran, and my two colleagues, Gilles Celeux and Jean Diebolt. The above derivation from the massive Gradsteyn and Ryzhik (which I discovered thanks to Mary Ellen Bock when arriving in Purdue) is indeed incorrect as the final term should be the square root of 2β rather than 8β. However, this typo does not impact the normalising constant of the density, K(α,μ,τ), unless I am further confused.

re-revisiting Jeffreys

Analytic Posteriors for Pearson’s Correlation Coefficient was arXived yesterday by Alexander Ly , Maarten Marsman, and Eric-Jan Wagenmakers from Amsterdam, with whom I recently had two most enjoyable encounters (and dinners!). And whose paper on Jeffreys’ Theory of Probability I recently discussed in the Journal of Mathematical Psychology.

The paper re-analyses Bayesian inference on the Gaussian correlation coefficient, demonstrating that for standard reference priors the posterior moments are (surprisingly) available in closed form. Including priors suggested by Jeffreys (in a 1935 paper), Lindley, Bayarri (Susie’s first paper!), Berger, Bernardo, and Sun. They all are of the form

and the corresponding profile likelihood on ρ is in “closed” form (“closed” because it involves hypergeometric functions). And only depends on the sample correlation which is then marginally sufficient (although I do not like this notion!). The posterior moments associated with those priors can be expressed as series (of hypergeometric functions). While the paper is very technical, borrowing from the Bateman project and from Gradshteyn and Ryzhik, I like it if only because it reminds me of some early papers I wrote in the same vein, Abramowitz and Stegun being one of the very first books I bought (at a ridiculous price in the bookstore of Purdue University…).

Two comments about the paper: I see nowhere a condition for the posterior to be proper, although I assume it could be the n>1+γ−2α+δ constraint found in Corollary 2.1 (although I am surprised there is no condition on the coefficient β). The second thing is about the use of this analytic expression in simulations from the marginal posterior on ρ: Since the density is available, numerical integration is certainly more efficient than Monte Carlo integration [for quantities that are not already available in closed form]. Furthermore, in the general case when β is not zero, the cost of computing infinite series of hypergeometric and gamma functions maybe counterbalanced by a direct simulation of ρ and both variance parameters since the profile likelihood of this triplet is truly in closed form, see eqn (2.11). And I will not comment the fact that Fisher ends up being the most quoted author in the paper!

Le Monde puzzle [#743]

As Le Monde weekend has yet again changed its format (with so much more advertisements for luxurious items that I sometimes wonder whether or not this is the weekend edition of Le Monde!], it took me a while to locate the mathematical puzzle. The good news is there now is a science&techno leaflet with, at the end, the math puzzle! (Sorry, this is of no relevance for anyone but me!)

The problem of last week is loosely connected with random walks on a grid. Given a nxm grid, consider all the shortest length paths linking (0,0) with (n,m). They all are of length n+m and can be represented as a sequence of l‘s and d‘s (for left and down). The question amounts to compute the probability that two of those paths intersect “in the middle”, i.e. after (n+m)/2 steps if (n+m) is even, or share the edge from the (n+m-1)/2 node to the  (n+m+1)/2 node.

When (n+m) is even, if the meeting node is (i,j), with i+j=(n+m)/2, there are

moves from (0,0) to (i,j) and then again

moves from (i,j) to (n,m) (since the total number of down moves is n). The number of paths going from (0,0) to (n,m) through (i,j) is therefore

and the probability of meeting in (i,j) is

hence the probability of meeting somewhere is

whose numerator is equal to

according to Wolfram alpha when n>m…. And to

otherwise. Nothing we can compute in R, I am afraid. (Feel free to process the case when n+m is odd as an exercise!)

Now, the original problem involved a random choice of direction (left and down) at each node (if any), meaning all paths do not have the same probability. So here is a (plain) R code aiming at approximating the probability:

N=10^3
n=7
m=11

genepath=function(n,m){

  path=matrix(0,ncol=2,nrow=n+m+1)

  for (t in 2:(n+m+1)){

    if (max(path[,1]-n,path[,2]-m)<0){
       path[t,]=path[t-1,]+sample(c(0,1),2)
       }else{
          path[t,]=path[t-1,]+c((path[t-1,1]<n),(path[t-1,2]<m))
          }}
  path
  }

cross=0
dega=hcl(h = seq(360, 340, length = N)+100,
       l = seq(90, 10, length = N))
par(mar=c(0,0,0,0))
plot(seq(0,n,le=100),seq(0,m,le=100),axes=FALSE,col="white",
     xlab="",ylab="")
for (a in 1:N){

  path1=genepath(n,m)
  path2=genepath(n,m)
  lww=.3 #width of path

  #signals intersections
  if ((path1[1+(n+m)/2,1]==path2[1+(n+m)/2,1])&&
      (path1[1+(n+m)/2,2]==path2[1+(n+m)/2,2])){
    points(jitter(path1[1+(n+m)/2,1]),jitter(path1[1+(n+m)/2,2]),
           col="sienna2",pch=19)
    cross=cross+1
    lww=1}

  #separates paths
  drift=jitter(path1-path2)
  lines(path2+drift,col=dega[a],lwd=lww)
  lines(path1-drift,col=dega[a],lwd=lww)
  }

cross/N