common leftovers

The Riddler was about a number game, which meant starting a sum at 0 and adding i to the current sum at time i, almost a Fibonacci sequence but not exactly, since the sequence is simply

which is easy to code, is of period 200, and this code showed that 3, 28, 53, and 78 were the most frequent last two digits. Or all 3 modulo 25 digits.

Tribonacci sequence

A simplistic puzzle from The Riddler when applying brute force:

A Tribonacci sequence is based on three entry integers a ≤ b ≤ c, and subsequent terms are the sum of the previous three. Among Tribonacci sequences containing 2023, which one achieves the smallest fourth term, a+b+c ?

The R code

tri<-function(a,b,e){
  while(F<2023){
  F=a+b+e;a=b;b=e;e=F}
  return(F<2024)}
sol=NULL;m=674
for(a in 1:m)
  for(b in a:m)
    for(e in b:m)
     if(tri(a,b,e)){
       sol=rbind(sol,c(a,b,e))}

leads to (1,1,6) as the solution… Incidentally, this short exercise led me to finally look for a fix to entering vectors as arguments of functions requesting lists:

do.call("tri",as.list(sol[2023,]))

puzzles & riddles

A rather simplistic game on the Riddler of 18 December:

…two players, each of whom starts with a whole number of points. Players take turns “attacking” each other, which involves subtracting their own number of points from their opponent’s until one of the players is out of points.

Easy to code in R:

g=function(N,M)ifelse(N<M,-g(M-N,N),1)

f=function(N,M=N){
  while(g(N,M)>0)M=M+1
  return(M)}

which converges to the separating ratio 1.618. If decomposing the actions until one player wins, one gets a sequence of upper and lower bounds associated with the Fibonacci sequence: 1⁻, 2⁺, 3/2⁻, 5/3⁺, 8/5⁻, &tc, converging to the “golden ratio” φ.

As an aside, I also solved a relatively quick codegolf challenge, where the question was to find the sum of all possible binary values from a bitmask. Meaning that for a binary input, e.g., 101X0XX0…01X, with some entries masked by X’s, one had to find the sum of all binary numbers compatible with the input. Which can be solved succinctly by counting the number of X’s, k, and adding the visible bits times and replacing the invisible ones by  . With some help, and using 2 instead of X, my R code moved from 158 bytes to 50:

function(x)2^sum(a<-x>1)*rev(x/4^a)%*%2^(seq(x)-1)

riddles on Egyptian fractions and Bernoulli factories

Two fairy different riddles on the weekend Riddler. The first one is (in fine) about Egyptian fractions: I understand the first one as

Find the Egyptian fraction decomposition of 2 into 11 distinct unit fractions that maximises the smallest fraction.

And which I cannot solve despite perusing this amazing webpage on Egyptian fractions and making some attempts at brute force  random exploration. Using Fibonacci’s greedy algorithm. I managed to find such decompositions

2 = 1 +1/2 +1/6 +1/12 +1/16 +1/20 +1/24 +1/30 +1/42 +1/48 +1/56

after seeing in this short note

2 = 1 +1/3 +1/5 +1/7 +1/9 +1/42 +1/15 +1/18 +1/30 +1/45 +1/90

And then Robin came with the following:

2 = 1 +1/4 +1/5 +1/8 +1/10 +1/12 +1/15 +1/20 +1/21 +1/24 +1/28

which may prove to be the winner! But there is even better:

2 = 1 +1/5 +1/6 +1/8 +1/9 +1/10 +1/12 +1/15 +1/18 +1/20 +1/24

The second riddle is a more straightforward Bernoulli factory problem:

Given a coin with a free-to-choose probability p of head, design an experiment with a fixed number k of draws that returns three outcomes with equal probabilities.

For which I tried a brute-force search of all possible 3-partitions of the 2-to-the-k events for a range of values of p from .01 to .5 and for k equal to 3,4,… But never getting an exact balance between the three groups. Reading later the solution on the Riddler, I saw that there was an exact solution for 4 draws when

Augmenting the precision of my solver (by multiplying all terms by 100), I indeed found a difference of

> solver((3-sqrt(3*(4*sqrt(6)-9)))/6,ba=1e5)[1]
[1] 8.940697e-08

which means an error of 9 x 100⁻⁴ x 10⁻⁸, ie roughly 10⁻¹⁵.

Le Monde puzzle [#1073]

And here is Le Monde mathematical puzzle  last competition problem

Find the number of integers such that their 15 digits are all between 1,2,3,4, and the absolute difference between two consecutive digits is 1. Among these numbers how many have 1 as their three-before-last digit and how many have 2?

Combinatorics!!! While it seems like a Gordian knot because the number of choices depends on whether or not a digit is an endpoint (1 or 4), there is a nice recurrence relation between the numbers of such integers with n digits and leftmost digit i, namely that

n⁴=(n-1)³, n³=(n-1)²+(n-1)⁴, n²=(n-1)²+(n-1)¹, n¹=(n-1)²

with starting values 1¹=1²=1³=1⁴=1 (and hopefully obvious notations). Hence it is sufficient to iterate the corresponding transition matrix

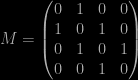
on this starting vector 14 times (with R, which does not enjoy a built-in matrix power) to end up with

15¹=610, 15²= 987, 15³= 987, 15⁴= 610

which leads to 3194 different numbers as the solution to the first question. As pointed out later by Amic and Robin in Dauphine, this happens to be twice Fibonacci’s sequence.

For the second question, the same matrix applies, with a different initial vector. Out of the 3+5+5+3=16 different integers with 4 digits, 3 start with 1 and 5 with 2. Then multiplying (3,0,0,0) by M¹⁰ leads to 267+165=432 different values for the 15 digit integers and multiplying (0,5,0,0) by M¹⁰ to. 445+720=1165 integers. (With the reassuring property that 432+1165 is half of 3194!) This is yet another puzzle in the competition that is of no special difficulty and with no further challenge going from the first to the second question…