reading classics (#1)

Here we are, back in a new school year and with new students reading the classics. Today, Ilaria Masiani started the seminar with a presentation of Spiegelhalter et al. 2002 DIC paper, already heavily mentioned on this blog. Here are the slides, posted on slideshare (if you know of another website housing and displaying slides, let me know: the incompatibility between Firefox and slideshare drives me crazy!, well, almost…)

I have already said a lot about DIC on this blog so will not add a repetition of my reservations. I enjoyed the link with the log scores and the Kullback-Leibler divergence, but failed to see a proper intuition for defining the effective number of parameters the way it is defined in the paper… The presentation was quite faithful to the original and, as is usual in the reading seminars (esp. the first one of the year), did not go far enough (for my taste) in the critical evaluation of the themes therein. Maybe an idea for next year would be to ask one of my PhD students to give the zeroth seminar…

Lindley’s paradox(es) and scores

“In the asymptotic limit, the Bayesian cannot justify the strictly positive probability of H₀ as an approximation to testing the hypothesis that the parameter value is close to θ₀ — which is the hypothesis of real scientific interest”

While revising my Jeffreys-Lindley’s paradox paper for Philosophy of Science, it was suggested (to me) that I read the incoming paper by Jan Sprenger on this paradox. The paper is entitled Testing a Precise Null Hypothesis: The Case of Lindley’s Paradox and it defends the thesis that the regular Bayesian approach (hence the Bayes factor used in the Jeffreys-Lindley’s paradox) is forced to put a prior on the (point) null hypothesis when all that really matters is the vicinity of the null. (I think Andrew would agree there as he positively hates point null hypotheses. See also Rissanen’s perspective about maximal precision allowed by a give sample.) Sprenger then advocates the use of the log score for comparing the full model with the point-null sub-model, i.e. the posterior expectation of the Kullback-Leibler distance between both models:

rejoining  José Bernardo and Phil Dawid on this ground.

While I agree about the notion that it is impossible to distinguish a small enough departure from the null from the null (no typo!), and I also support the argument that “all models are wrong”, hence point null should eventually—meaning with enough data—rejected, I find the Bayesian solution through the Bayes factor rather appealing because it uses the prior distribution to weight the alternative values of θ in order to oppose their averaged likelihood to the likelihood in θ₀. (Note I did not mention Occam!) Further, while the notion of opposing a point null to the rest of the Universe may sound silly, what truly matters is the decisional setting, namely that we want to select a simpler model and use it for later purposes. It is therefore this issue that should be tested, rather than whether or not θ is exactly equal to θ₀. I incidentally find it amusing that Sprenger picks the ESP experiment as his illustration in that this is a (the?) clearcut case where the point null: “there is no such thing as ESP” makes sense. Now, it can be argued that what the statistical experiment is assessing is the ESP experiment, for which many objective causes (beyond ESP!) may induce a departure from the null (and from the binomial model). But then this prevents any rational analysis of the test (as is indeed the case!).

The paper thus objects to the use of Bayes factors (and of p-values) to instead  propose to compare scores in the Bernardo-Dawid spirit. As discussed earlier, it has several appealing features, from recovering the Kullback-Leibler divergence between models as a measure of fit  to allowing for the incorporation of improper priors (a point Andrew may disagree with), to avoiding the double use of the data. It is however incomplete in that it creates a discrepancy or a disbalance between both models, thus making the comparison of more than two models difficult to fathom, and it does not readily incorporate the notion of nuisance parameters in the embedded model, seemingly forcing the inclusion of pseudo-priors as in the Bayesian analysis of Aitkin’s integrated likelihood.

workshop a Padova (#2)

This morning session at the workshop Recent Advances in statistical inference: theory and case studies was a true blessing for anyone working in Bayesian model choice! And it did give me ideas to complete my current paper on the Jeffreys-Lindley paradox, and more. Attending the talks in the historical Gioachino Rossini room of the fabulous Café Pedrocchi with the Italian spring blue sky as a background surely helped! (It is only beaten by this room of Ca’Foscari overlooking the Gran Canale where we had a workshop last Fall…)

First, Phil Dawid gave a talk on his current work with Monica Musio (who gave a preliminary talk on this in Venezia last fall) on the use of new score functions to compare statistical models. While the regular Bayes factor is based on the log score, comparing the logs of the predictives at the observed data, different functions of the predictive q can be used, like the Hyvärinen score

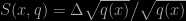
which offers the immense advantage of being independent of the normalising constant and hence can also be used for improper priors. As written above, a very deep finding that could at last allow for the comparison of models based on improper priors without requiring convoluted constructions (see below) to make the “constants meet”. I first thought the technique was suffering from the same shortcoming as Murray Aitkin’s integrated likelihood, but I eventually figured out (where) I was wrong!

The second talk was given by Ed George, who spoke on his recent research with Veronika Rocková dealing with variable selection via an EM algorithm that proceeds much much faster to the optimal collection of variables, when compared with the DMVS solution of George and McCulloch (JASA, 1993). (I remember discussing this paper with Ed in Laramie during the IMS meeting in the summer of 1993.) This resurgence of the EM algorithm in this framework is both surprising (as the missing data structure represented by the variable indicators could have been exploited much earlier) and exciting, because it opens a new way to explore the most likely models in this variable selection setting and to eventually produce the median model of Berger and Barbieri (Annals of Statistics, 2004). In addition, this approach allows for a fast comparison of prior modellings on the missing variable indicators, showing in some examples a definitive improvement brought by a Markov random field structure. Given that it also produces a marginal posterior density on the indicators, values of hyperparameters can be assessed, escaping the Jeffreys-Lindley paradox (which was clearly a central piece of today’s talks and discussions). I would like to see more details on the MRF part, as I wonder which structure is part of the input and which one is part of the inference.

The third talk of the morning was Susie Bayarri’s, about a collection of desiderata or criteria for building an objective prior in model comparison and achieving a manageable closed-form solution in the case of the normal linear model. While I somehow disagree with the information criterion, which states that the divergence of the likelihood ratio should imply a corresponding divergence of the Bayes factor. While I definitely agree with the invariance argument leading to using the same (improper) prior over parameters common to models under comparison, this may sound too much of a trick to outsiders, especially when accounting for the score solution of Dawid and Musio. Overall, though, I liked the outcome of a coherence reference solution for linear models that could clearly be used as a default in this setting, esp. given the availability of an R package called BayesVarSel. (Even if I also like our simpler solution developped in the incoming edition of Bayesian Core, also available in the bayess R package!) In his discussion, Guido Consonni highlighted the philosophical problem of considering “common paramaters”, a perspective I completely subscribe to, even though I think all that matters is the justification of having a common prior over formally equivalent parameters, even though this may sound like a pedantic distinction to many!

Due to a meeting of the scientific committee of the incoming O’Bayes 2013 meeting (in Duke, December, more about this soon!), whose most members were attending this workshop, I missed the beginning of Alan Aggresti’s talk and could not catch up with the central problem he was addressing (the pianist on the street outside started pounding on his instrument as if intent to break it apart!). A pity as problems with contingency tables are certainly of interest to me… By the end of Alan’s talk, I wished someone would shoot the pianist playing outside (even though he was reasonably gifted) as I had gotten a major headache from his background noise. Following Noel Cressie’s talk proved just as difficult, although I could see his point in comparing very diverse predictors for big Data problems without much of a model structure and even less of a  and I decided to call the day off, despite wishing to stay for Eduardo Gutiérrez-Pena’s talk on conjugate predictives and entropies which definitely interested me… Too bad really (blame the pianist!)