Here is a picture seen in a Nature Reviews Physics paper I came across, on the Hubble constant being consistently estimated as large now than previously. I have no informed comment to make on the paper, which thinks that these discrepancies support altering the composition of the Universe shortly before the emergence of the Cosmological Background Noise (CMB), but the way it presented the confidence assessments of the same constant H⁰ based on 13 different experiments is rather ghastly, from using inclined confidence intervals, to adding a USA Today touch to the graph via a broken bridge and a river below, to resorting to different scales for both parts of the bridge… 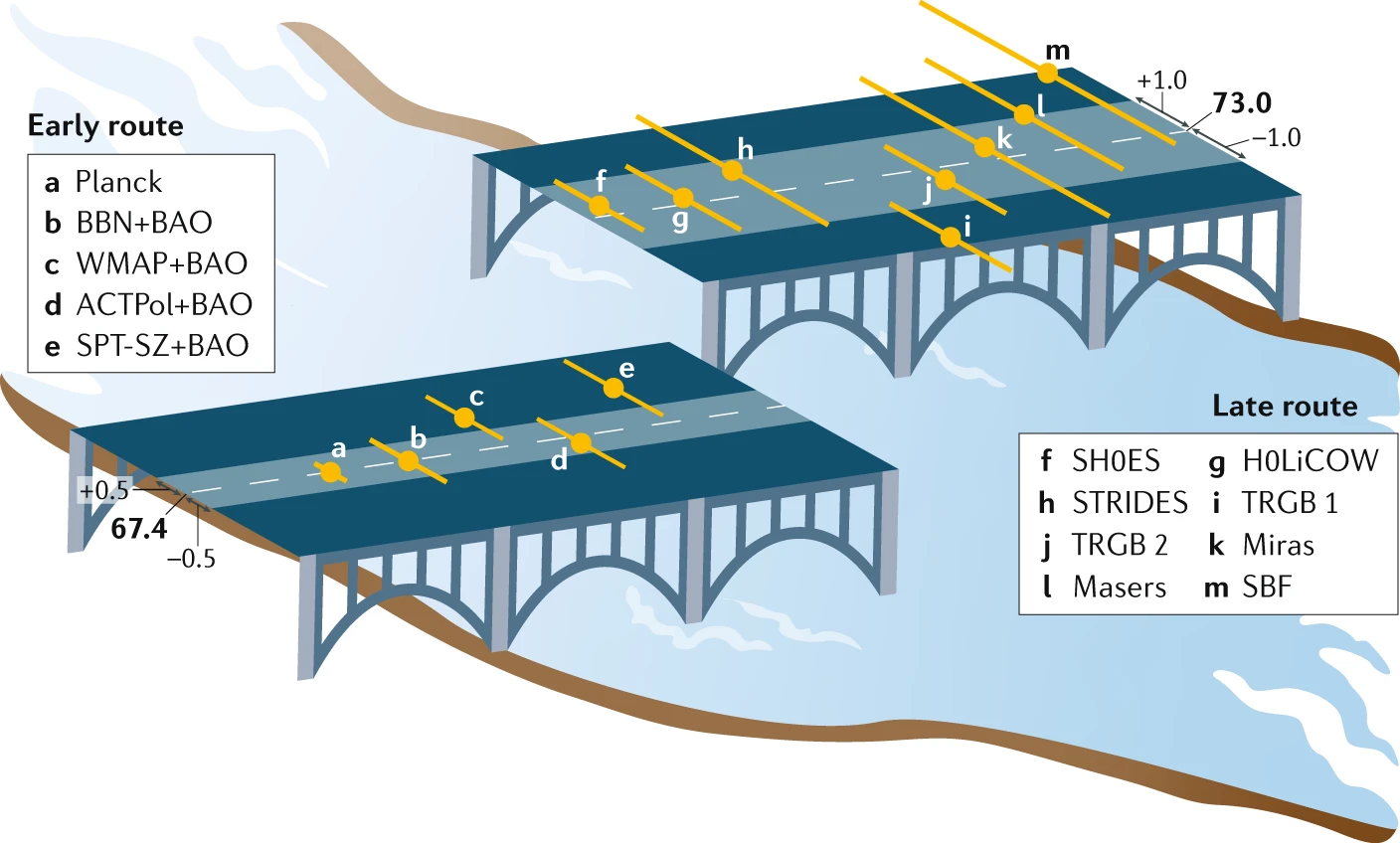
Archive for cosmology
a bad graph about Hubble discrepancies
Posted in Books, pictures, Statistics, Travel, University life with tags bad graph, CMB, cosmology, Hubble constant, Nature Reviews Physics on September 23, 2020 by xi'ansimulated summary statistics [in the sky]
Posted in Statistics with tags ABC, approximate likelihood, Bayes factor, computer-simulated model, cosmology, cosmostats, de-biasing, urbi et orbi on October 10, 2018 by xi'an Thinking it was related with ABC, although in the end it is not!, I recently read a baffling cosmology paper by Jeffrey and Abdalla. The data d there means an observed (summary) statistic, while the summary statistic is a transform of the parameter, μ(θ), which calibrates the distribution of the data. With nuisance parameters. More intriguing to me is the sentence that the correct likelihood of d is indexed by a simulated version of μ(θ), μ'(θ), rather than by μ(θ). Which seems to assume that the pseudo- or simulated data can be produced for the same value of the parameter as the observed data. The rest of the paper remains incomprehensible for I do not understand how the simulated versions are simulated.
Thinking it was related with ABC, although in the end it is not!, I recently read a baffling cosmology paper by Jeffrey and Abdalla. The data d there means an observed (summary) statistic, while the summary statistic is a transform of the parameter, μ(θ), which calibrates the distribution of the data. With nuisance parameters. More intriguing to me is the sentence that the correct likelihood of d is indexed by a simulated version of μ(θ), μ'(θ), rather than by μ(θ). Which seems to assume that the pseudo- or simulated data can be produced for the same value of the parameter as the observed data. The rest of the paper remains incomprehensible for I do not understand how the simulated versions are simulated.
“…the corrected likelihood is more than a factor of exp(30) more probable than the uncorrected. This is further validation of the corrected likelihood; the model (i.e. the corrected likelihood) shows a better goodness-of-fit.”
The authors further ressort to Bayes factors to compare corrected and uncorrected versions of the likelihoods, which leads (see quote) to picking the corrected version. But are they comparable as such, given that the corrected version involves simulations that are treated as supplementary data? As noted by the authors, the Bayes factor unsurprisingly goes to one as the number M of simulations grows to infinity, as supported by the graph below.
ABC²DE
Posted in Books, Statistics with tags ABC, ABC algorithm, Carnegie Mellon University, CMU, conditional density, cosmology, Edinburgh, FlexCode, IAP, local regression, local scaling, Monte Carlo error, non-parametric kernel estimation, reference table on June 25, 2018 by xi'an A recent arXival on a new version of ABC based on kernel estimators (but one could argue that all ABC versions are based on kernel estimators, one way or another.) In this ABC-CDE version, Izbicki, Lee and Pospisilz [from CMU, hence the picture!] argue that past attempts failed to exploit the full advantages of kernel methods, including the 2016 ABCDE method (from Edinburgh) briefly covered on this blog. (As an aside, CDE stands for conditional density estimation.) They also criticise these attempts at selecting summary statistics and hence failing in sufficiency, which seems a non-issue to me, as already discussed numerous times on the ‘Og. One point of particular interest in the long list of drawbacks found in the paper is the inability to compare several estimates of the posterior density, since this is not directly ingrained in the Bayesian construct. Unless one moves to higher ground by calling for Bayesian non-parametrics within the ABC algorithm, a perspective which I am not aware has been pursued so far…
A recent arXival on a new version of ABC based on kernel estimators (but one could argue that all ABC versions are based on kernel estimators, one way or another.) In this ABC-CDE version, Izbicki, Lee and Pospisilz [from CMU, hence the picture!] argue that past attempts failed to exploit the full advantages of kernel methods, including the 2016 ABCDE method (from Edinburgh) briefly covered on this blog. (As an aside, CDE stands for conditional density estimation.) They also criticise these attempts at selecting summary statistics and hence failing in sufficiency, which seems a non-issue to me, as already discussed numerous times on the ‘Og. One point of particular interest in the long list of drawbacks found in the paper is the inability to compare several estimates of the posterior density, since this is not directly ingrained in the Bayesian construct. Unless one moves to higher ground by calling for Bayesian non-parametrics within the ABC algorithm, a perspective which I am not aware has been pursued so far…
The selling points of ABC-CDE are that (a) the true focus is on estimating a conditional density at the observable x⁰ rather than everywhere. Hence, rejecting simulations from the reference table if the pseudo-observations are too far from x⁰ (which implies using a relevant distance and/or choosing adequate summary statistics). And then creating a conditional density estimator from this subsample (which makes me wonder at a double use of the data).
The specific density estimation approach adopted for this is called FlexCode and relates to an earlier if recent paper from Izbicki and Lee I did not read. As in many other density estimation approaches, they use an orthonormal basis (including wavelets) in low dimension to estimate the marginal of the posterior for one or a few components of the parameter θ. And noticing that the posterior marginal is a weighted average of the terms in the basis, where the weights are the posterior expectations of the functions themselves. All fine! The next step is to compare [posterior] estimators through an integrated squared error loss that does not integrate the prior or posterior and does not tell much about the quality of the approximation for Bayesian inference in my opinion. It is furthermore approximated by a doubly integrated [over parameter and pseudo-observation] squared error loss, using the ABC(ε) sample from the prior predictive. And the approximation error only depends on the regularity of the error, that is the difference between posterior and approximated posterior. Which strikes me as odd, since the Monte Carlo error should take over but does not appear at all. I am thus unclear as to whether or not the convergence results are that relevant. (A difficulty with this paper is the strong dependence on the earlier one as it keeps referencing one version or another of FlexCode. Without reading the original one, I spotted a mention made of the use of random forests for selecting summary statistics of interest, without detailing the difference with our own ABC random forest papers (for both model selection and estimation). For instance, the remark that “nuisance statistics do not affect the performance of FlexCode-RF much” reproduces what we observed with ABC-RF.
The long experiment section always relates to the most standard rejection ABC algorithm, without accounting for the many alternatives produced in the literature (like Li and Fearnhead, 2018. that uses Beaumont et al’s 2002 scheme, along with importance sampling improvements, or ours). In the case of real cosmological data, used twice, I am uncertain of the comparison as I presume the truth is unknown. Furthermore, from having worked on similar data a dozen years ago, it is unclear why ABC is necessary in such context (although I remember us running a test about ABC in the Paris astrophysics institute once).
Stephen Hawking (1942-2018)
Posted in Books, University life with tags A brief history of time, Cambridge University, cosmology, Death, fairy story, quotes, Stephen Hawking on March 14, 2018 by xi'an
“I have lived with the prospect of an early death for the last 49 years. I’m not afraid of death, but I’m in no hurry to die. I have so much I want to do first. I regard the brain as a computer which will stop working when its components fail. There is no heaven or afterlife for broken down computers; that is a fairy story for people afraid of the dark.”
Astrostatistics school
Posted in Mountains, pictures, R, Statistics, Travel, University life with tags ABC, ABC model choice, abcrf, abctools package, Alps, astronomy, Autrans, Bayesian inference, Bayesian Methods in Cosmology, big wall, cosmology, Dickey-Savage ratio, Fall, mountains, nested sampling, R, random forests, rock climbing, RStudio, socks, trail running, Vercors on October 17, 2017 by xi'an What a wonderful week at the Astrostat [Indian] summer school in Autrans! The setting was superb, on the high Vercors plateau overlooking both Grenoble [north] and Valence [west], with the colours of the Fall at their brightest on the foliage of the forests rising on both sides of the valley and a perfect green on the fields at the centre, with sun all along, sharp mornings and warm afternoons worthy of a late Indian summer, too many running trails [turning into X country ski trails in the Winter] to contemplate for a single week [even with three hours of running over two days], many climbing sites on the numerous chalk cliffs all around [but a single afternoon for that, more later in another post!]. And of course a group of participants eager to learn about Bayesian methodology and computational algorithms, from diverse [astronomy, cosmology and more] backgrounds, trainings and countries. I was surprised at the dedication of the participants travelling all the way from Chile, Péru, and Hong Kong for the sole purpose of attending the school. David van Dyk gave the first part of the school on Bayesian concepts and MCMC methods, Roberto Trotta the second part on Bayesian model choice and hierarchical models, and myself a third part on, surprise, surprise!, approximate Bayesian computation. Plus practicals on R.
What a wonderful week at the Astrostat [Indian] summer school in Autrans! The setting was superb, on the high Vercors plateau overlooking both Grenoble [north] and Valence [west], with the colours of the Fall at their brightest on the foliage of the forests rising on both sides of the valley and a perfect green on the fields at the centre, with sun all along, sharp mornings and warm afternoons worthy of a late Indian summer, too many running trails [turning into X country ski trails in the Winter] to contemplate for a single week [even with three hours of running over two days], many climbing sites on the numerous chalk cliffs all around [but a single afternoon for that, more later in another post!]. And of course a group of participants eager to learn about Bayesian methodology and computational algorithms, from diverse [astronomy, cosmology and more] backgrounds, trainings and countries. I was surprised at the dedication of the participants travelling all the way from Chile, Péru, and Hong Kong for the sole purpose of attending the school. David van Dyk gave the first part of the school on Bayesian concepts and MCMC methods, Roberto Trotta the second part on Bayesian model choice and hierarchical models, and myself a third part on, surprise, surprise!, approximate Bayesian computation. Plus practicals on R.
 As it happens Roberto had to cancel his participation and I turned for a session into Christian Roberto, presenting his slides in the most objective possible fashion!, as a significant part covered nested sampling and Savage-Dickey ratios, not exactly my favourites for estimating constants. David joked that he was considering postponing his flight to see me talk about these, but I hope I refrained from engaging into controversy and criticisms… If anything because this was not of interest for the participants. Indeed when I started presenting ABC through what I thought was a pedestrian example, namely Rasmus Baath’s socks, I found that the main concern was not running an MCMC sampler or a substitute ABC algorithm but rather an healthy questioning of the construction of the informative prior in that artificial setting, which made me quite glad I had planned to cover this example rather than an advanced model [as, e.g., one of those covered in the packages abc, abctools, or abcrf]. Because it generated those questions about the prior [why a Negative Binomial? why these hyperparameters? &tc.] and showed how programming ABC turned into a difficult exercise even in this toy setting. And while I wanted to give my usual warning about ABC model choice and argue for random forests as a summary selection tool, I feel I should have focussed instead on another example, as this exercise brings out so clearly the conceptual difficulties with what is taught. Making me quite sorry I had to leave one day earlier. [As did missing an extra run!] Coming back by train through the sunny and grape-covered slopes of Burgundy hills was an extra reward [and no one in the train commented about the local cheese travelling in my bag!]
As it happens Roberto had to cancel his participation and I turned for a session into Christian Roberto, presenting his slides in the most objective possible fashion!, as a significant part covered nested sampling and Savage-Dickey ratios, not exactly my favourites for estimating constants. David joked that he was considering postponing his flight to see me talk about these, but I hope I refrained from engaging into controversy and criticisms… If anything because this was not of interest for the participants. Indeed when I started presenting ABC through what I thought was a pedestrian example, namely Rasmus Baath’s socks, I found that the main concern was not running an MCMC sampler or a substitute ABC algorithm but rather an healthy questioning of the construction of the informative prior in that artificial setting, which made me quite glad I had planned to cover this example rather than an advanced model [as, e.g., one of those covered in the packages abc, abctools, or abcrf]. Because it generated those questions about the prior [why a Negative Binomial? why these hyperparameters? &tc.] and showed how programming ABC turned into a difficult exercise even in this toy setting. And while I wanted to give my usual warning about ABC model choice and argue for random forests as a summary selection tool, I feel I should have focussed instead on another example, as this exercise brings out so clearly the conceptual difficulties with what is taught. Making me quite sorry I had to leave one day earlier. [As did missing an extra run!] Coming back by train through the sunny and grape-covered slopes of Burgundy hills was an extra reward [and no one in the train commented about the local cheese travelling in my bag!]
