Mars attack [live]

black holes capture Nobel

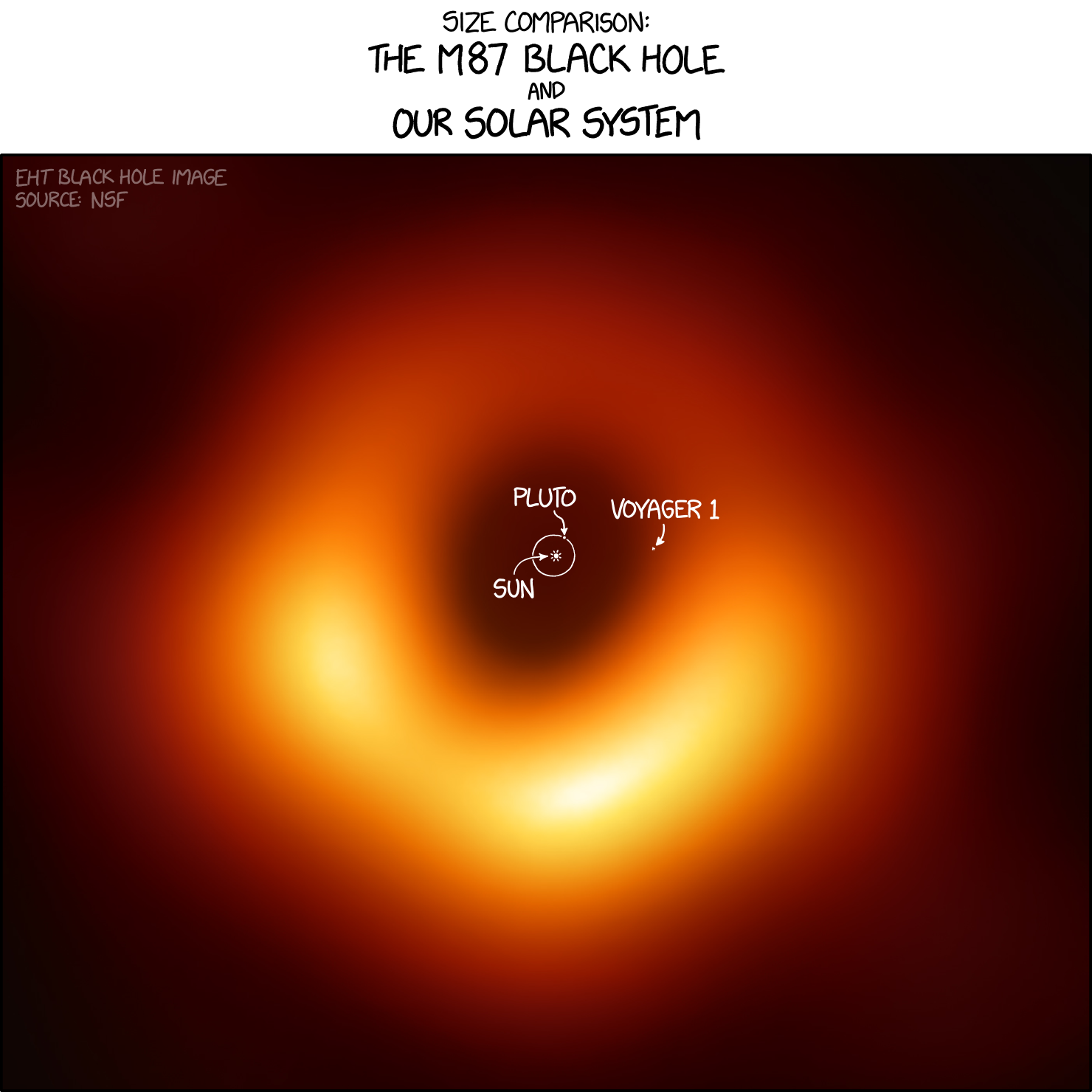
size matters

improperties on an astronomical scale

As pointed out by Peter Coles on his blog, In the Dark, Hyungsuk Tak, Sujit Ghosh, and Justin Ellis just arXived a review of the unsafe use of improper priors in astronomy papers, 24 out of 75 having failed to establish that the corresponding posteriors are well-defined. And they exhibit such an instance (of impropriety) in a MNRAS paper by Pihajoki (2017), which is a complexification of Gelfand et al. (1990), also used by Jim Hobert in his thesis. (Even though the formal argument used to show the impropriety of the posterior in Pihajoki’s paper does not sound right since it considers divergence at a single value of a parameter β.) Besides repeating this warning about an issue that was rather quickly identified in the infancy of MCMC, if not in the very first publications on the Gibbs sampler, the paper seems to argue against using improper priors due to this potential danger, stating that instead proper priors that include all likely values and beyond are to be preferred. Which reminds me of the BUGS feature of using a N(0,10⁹) prior instead of the flat prior, missing the fact that “very large” variances do impact the resulting inference (if only for the issue of model comparison, remember Lindley-Jeffreys!). And are informative in that sense. However, it is obviously a good idea to advise checking for propriety (!) and using such alternatives may come as a safety button, providing a comparison benchmark to spot possible divergences in the resulting inference.

Astrostatistics school

What a wonderful week at the Astrostat [Indian] summer school in Autrans! The setting was superb, on the high Vercors plateau overlooking both Grenoble [north] and Valence [west], with the colours of the Fall at their brightest on the foliage of the forests rising on both sides of the valley and a perfect green on the fields at the centre, with sun all along, sharp mornings and warm afternoons worthy of a late Indian summer, too many running trails [turning into X country ski trails in the Winter] to contemplate for a single week [even with three hours of running over two days], many climbing sites on the numerous chalk cliffs all around [but a single afternoon for that, more later in another post!]. And of course a group of participants eager to learn about Bayesian methodology and computational algorithms, from diverse [astronomy, cosmology and more] backgrounds, trainings and countries. I was surprised at the dedication of the participants travelling all the way from Chile, Péru, and Hong Kong for the sole purpose of attending the school. David van Dyk gave the first part of the school on Bayesian concepts and MCMC methods, Roberto Trotta the second part on Bayesian model choice and hierarchical models, and myself a third part on, surprise, surprise!, approximate Bayesian computation. Plus practicals on R.

As it happens Roberto had to cancel his participation and I turned for a session into Christian Roberto, presenting his slides in the most objective possible fashion!, as a significant part covered nested sampling and Savage-Dickey ratios, not exactly my favourites for estimating constants. David joked that he was considering postponing his flight to see me talk about these, but I hope I refrained from engaging into controversy and criticisms… If anything because this was not of interest for the participants. Indeed when I started presenting ABC through what I thought was a pedestrian example, namely Rasmus Baath’s socks, I found that the main concern was not running an MCMC sampler or a substitute ABC algorithm but rather an healthy questioning of the construction of the informative prior in that artificial setting, which made me quite glad I had planned to cover this example rather than an advanced model [as, e.g., one of those covered in the packages abc, abctools, or abcrf]. Because it generated those questions about the prior [why a Negative Binomial? why these hyperparameters? &tc.] and showed how programming ABC turned into a difficult exercise even in this toy setting. And while I wanted to give my usual warning about ABC model choice and argue for random forests as a summary selection tool, I feel I should have focussed instead on another example, as this exercise brings out so clearly the conceptual difficulties with what is taught. Making me quite sorry I had to leave one day earlier. [As did missing an extra run!] Coming back by train through the sunny and grape-covered slopes of Burgundy hills was an extra reward [and no one in the train commented about the local cheese travelling in my bag!]