Iran [cover]

MaxEnt im Garching

The next edition of the MaxEnt conferences, or more precisely workshops on Bayesian Inference and Maximum Entropy Methods in Science and Engineering , MaxEnt2023, will take place in Garching (bei München) next 3-7 July. At the Max-Planck-Institut für Plasmaphysik. While the conference is usually of strong interest, it is rather improbable I will attend it this year. (The only time I took part in a MaxEnt conference was in 2009, in Oxford. Oxford, Mississippi!).

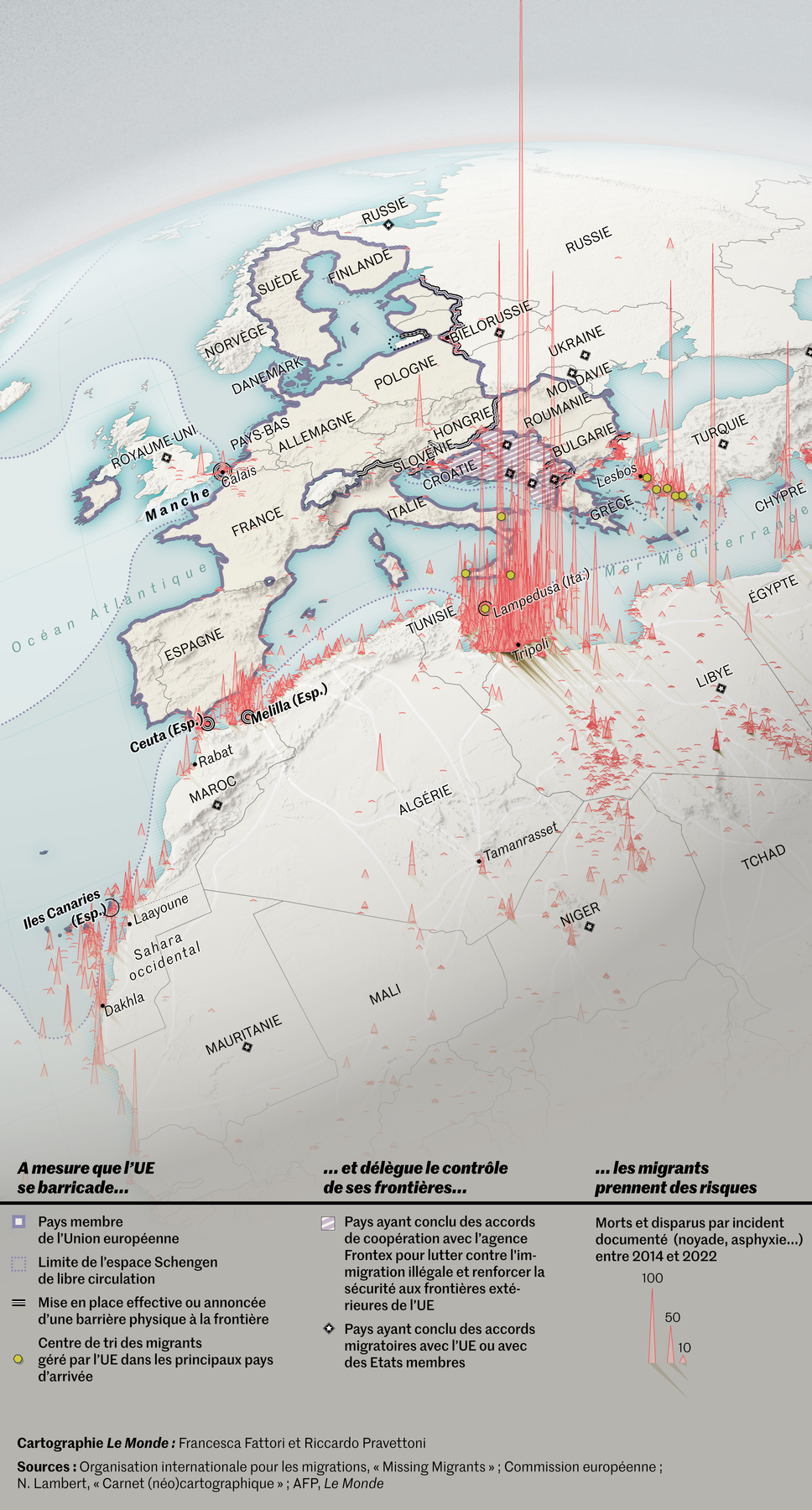
borderline deaths

nothing’s sacred [Charlie Hebdo repost]

[Reposted a tribune by the Charlie Hebdo writers in Le Monde, 15 August]

The assassination attempt on Salman Rushdie is a reminder to those who seem to have forgotten that the basic freedoms of modern society, such as the freedom to create and express oneself, are constantly threatened by totalitarian ideologies around the world.

These hateful and contemptuous ideologies are based on political or religious theories whose self-proclaimed legitimacy raises questions. Salman Rushdie’s case forces us to question the place of religion and sacredness in our modern world.

If freedom of conscience gives each person the right to think what he or she wants about the origin of the world and its creation, the truths of religious revelation cannot impose their precepts on the whole of society. But for several years, we have noticed that religious practices are becoming more and more intrusive and authoritarian – when they are not outright threatening. This slippery slope seriously affects the subtle balance of democratic societies and creates a climate of insecurity, intimidation and violence that is no longer acceptable.

This is the goal of religious fanatics: to dissuade, through terror, the creation of works that challenge their dogmas, which are based on little more than a few visions from great mystics.

Can our modern societies be built around texts written by exalted minds? Nothing is sacred. The paradox is that today the mobilization to condemn the attack on Salman Rushdie seems stronger than the mobilization of artists to continue producing works that will perpetuate his vision. After those who have already been murdered, like Theo Van Gogh, and those who get stabbed during lectures, like Salman Rushdie, who will be left to continue their thinking and their struggle?

While global warming endangers living organisms on Earth, religious intolerance and unbridled mysticism threaten minds by suffocating them with prohibitions and irrevocable sentences.

To those who repeat: “We love death as much as you love life”, we must oppose limitless creativity and incessant insolence. No amount of moderation will allow us to enjoy the slightest indulgence from fanatics. The response must not only be political, through laws that protect freedoms and repress those who attack them. It must also be cultural and intellectual. We must never cease to challenge, using arguments and ideas, the dogmas and narratives of these so-called “sacred” books, which seek only to burn all others and to put to death those who wrote them.

the wgaf-value

While the special health council for the French Government is closing down, the number of cases here remains quite high, seemingly in a complete indifference or worse… When 25 000 persons died from COVID since January. But political parties are all (!) against any constraining measure, with some even calling in a most demagogic manner for reintegrating [the few hundred] unvaccinated public health personnel in the public health system… (As a single datapoint, take the counter-example of our thrice-vaccinated daughter who caught COVID last week, most likely when working at the hospital.)