are profile likelihoods likelihoods?!

A recent arXived paper by Oliver J. Maclaren is asking this very question. And argue for a positive answer. One of the invoked sources is Murray Aitkin’s integrated likelihood book, which I criticised here and elsewhere. With the idea of the paper being that

“….there is an appropriate notion of integration over variables that takes likelihood functions to likelihood functions via maximization.”

Hmm…. The switch there is to replace addition with maximisation, probability with possibility, and… profile likelihood as marginal possibility under this new concept. I just do not see how adapting these concepts for the interpretation of the profile likelihood makes the latter more meaningful, since it still overwhelmingly does not result from a distribution density at an observed realisation of a random variable. This reminds me a paper I refereed quite a long while ago where the authors were using Schwarz’ theory of distributions to expand the notion of unbiasedness. With unclear consequences.

Bayes is typically wrong…

In Harvard, this morning, Don Fraser gave a talk at the Bayesian, Fiducial, and Frequentist conference where he repeated [as shown by the above quote] the rather harsh criticisms on Bayesian inference he published last year in Statistical Science. And which I discussed a few days ago. The “wrongness” of Bayes starts with the completely arbitrary choice of the prior, which Don sees as unacceptable, and then increases because the credible regions are not confident regions, outside natural parameters from exponential families (Welch and Peers, 1963). And one-dimensional parameters using the profile likelihood (although I cannot find a proper definition of what the profile likelihood is in the paper, apparently a plug-in version that is not a genuine likelihood, hence somewhat falling under the same this-is-not-a-true-probability cleaver as the disputed Bayesian approach).

“I expect we’re all missing something, but I do not know what it is.” D.R. Cox, Statistical Science, 1994

And then Nancy Reid delivered a plenary lecture “Are we converging?” on the afternoon that compared most principles (including objective if not subjective Bayes) against different criteria, like consistency, nuisance elimination, calibration, meaning of probability, and so on.  In an highly analytic if pessimistic panorama. (The talk should be available on line at some point soon.)

re-revisiting Jeffreys

Analytic Posteriors for Pearson’s Correlation Coefficient was arXived yesterday by Alexander Ly , Maarten Marsman, and Eric-Jan Wagenmakers from Amsterdam, with whom I recently had two most enjoyable encounters (and dinners!). And whose paper on Jeffreys’ Theory of Probability I recently discussed in the Journal of Mathematical Psychology.

The paper re-analyses Bayesian inference on the Gaussian correlation coefficient, demonstrating that for standard reference priors the posterior moments are (surprisingly) available in closed form. Including priors suggested by Jeffreys (in a 1935 paper), Lindley, Bayarri (Susie’s first paper!), Berger, Bernardo, and Sun. They all are of the form

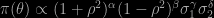
and the corresponding profile likelihood on ρ is in “closed” form (“closed” because it involves hypergeometric functions). And only depends on the sample correlation which is then marginally sufficient (although I do not like this notion!). The posterior moments associated with those priors can be expressed as series (of hypergeometric functions). While the paper is very technical, borrowing from the Bateman project and from Gradshteyn and Ryzhik, I like it if only because it reminds me of some early papers I wrote in the same vein, Abramowitz and Stegun being one of the very first books I bought (at a ridiculous price in the bookstore of Purdue University…).

Two comments about the paper: I see nowhere a condition for the posterior to be proper, although I assume it could be the n>1+γ−2α+δ constraint found in Corollary 2.1 (although I am surprised there is no condition on the coefficient β). The second thing is about the use of this analytic expression in simulations from the marginal posterior on ρ: Since the density is available, numerical integration is certainly more efficient than Monte Carlo integration [for quantities that are not already available in closed form]. Furthermore, in the general case when β is not zero, the cost of computing infinite series of hypergeometric and gamma functions maybe counterbalanced by a direct simulation of ρ and both variance parameters since the profile likelihood of this triplet is truly in closed form, see eqn (2.11). And I will not comment the fact that Fisher ends up being the most quoted author in the paper!