max vs. min

Another intriguing question on X validated (about an exercise in Jun Shao’s book) that made me realise a basic fact about exponential distributions. When considering two Exponential random variables X and Y with possibly different parameters λ and μ,  Z⁺=max{X,Y} is dependent on the event X>Y while Z⁻=min{X,Y} is not (and distributed as an Exponential variate with parameter λ+μ.) Furthermore, Z⁺ is distributed from a signed mixture

conditionally on the event X>Y, meaning that there is no sufficient statistic of fixed dimension when given a sample of n realisations of Z⁺’s along with the indicators of the events X>Y…. This may explain why there exists an unbiased estimator of λ⁻¹-μ⁻¹ in this case and (apparently) not when replacing Z⁺ by Z⁻. (Even though the exercise asks for the UMVUE.)

inverse Gaussian trick [or treat?]

When preparing my mid-term exam for my undergrad mathematical statistics course, I wanted to use the inverse Gaussian distribution IG(μ,λ) as an example of exponential family and include a random generator question. As shown above by a Fortran computer code from Michael, Schucany and Haas, a simple version can be based on simulating a χ²(1) variate and solving in x the following second degree polynomial equation

since the left-hand side transform is distributed as a χ²(1) random variable. The smallest root x¹, less than μ, is then chosen with probability μ/(μ+x¹) and the largest one, x²=μ²/x¹ with probability x¹/(μ+x¹). A relatively easy question then, except when one considers asking for the proof of the χ²(1) result, which proved itself to be a harder cookie than expected! The paper usually referred to for the result, Schuster (1968), is quite cryptic on the matter, essentially stating that the above can be expressed as the (bijective) transform of Y=min(X,μ²/X) and that V~χ²(1) follows immediately. I eventually worked out a proof by the “law of the unconscious statistician” [a name I do not find particularly amusing!], but did not include the question in the exam. But I found it fairly interesting that the inverse Gaussian can be generating by “inverting” the above equation, i.e. going from a (squared) Gaussian variate V to the inverse Gaussian variate X. (Even though the name stems from the two cumulant generating functions being inverses of one another.)

independent component analysis and p-values

Last morning at the neuroscience workshop Jean-François Cardoso presented independent component analysis though a highly pedagogical and enjoyable tutorial that stressed the geometric meaning of the approach, summarised by the notion that the (ICA) decomposition

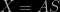
of the data X seeks both independence between the columns of S and non-Gaussianity. That is, getting as away from Gaussianity as possible. The geometric bits came from looking at the Kullback-Leibler decomposition of the log likelihood

where the expectation is computed under the true distribution P of the data X. And Q_θ is the hypothesised distribution. A fine property of this decomposition is a statistical version of Pythagoreas’ theorem, namely that when the family of Q_θ‘s is an exponential family, the Kullback-Leibler distance decomposes into

where θ⁰ is the expected maximum likelihood estimator of θ. (We also noticed this possibility of a decomposition in our Kullback-projection variable-selection paper with Jérôme Dupuis.) The talk by Aapo Hyvärinen this morning was related to Jean-François’ in that it used ICA all the way to a three-level representation if oriented towards natural vision modelling in connection with his book and the paper on unormalised models recently discussed on the ‘Og.

On the afternoon, Eric-Jan Wagenmaker [who persistently and rationally fight the (ab)use of p-values and who frequently figures on Andrew’s blog] gave a warning tutorial talk about the dangers of trusting p-values and going fishing for significance in existing studies, much in the spirit of Andrew’s blog (except for the defence of Bayes factors). Arguing in favour of preregistration. The talk was full of illustrations from psychology. And included the line that ESP testing is the jester of academia, meaning that testing for whatever form of ESP should be encouraged as a way to check testing procedures. If a procedure finds a significant departure from the null in this setting, there is something wrong with it! I was then reminded that Eric-Jan was one of the authors having analysed Bem’s controversial (!) paper on the “anomalous processes of information or energy transfer that are currently unexplained in terms of known physical or biological mechanisms”… (And of the shocking talk by Jessica Utts on the same topic I attended in Australia two years ago.)