max vs. min

Another intriguing question on X validated (about an exercise in Jun Shao’s book) that made me realise a basic fact about exponential distributions. When considering two Exponential random variables X and Y with possibly different parameters λ and μ,  Z⁺=max{X,Y} is dependent on the event X>Y while Z⁻=min{X,Y} is not (and distributed as an Exponential variate with parameter λ+μ.) Furthermore, Z⁺ is distributed from a signed mixture

conditionally on the event X>Y, meaning that there is no sufficient statistic of fixed dimension when given a sample of n realisations of Z⁺’s along with the indicators of the events X>Y…. This may explain why there exists an unbiased estimator of λ⁻¹-μ⁻¹ in this case and (apparently) not when replacing Z⁺ by Z⁻. (Even though the exercise asks for the UMVUE.)

statistics for making decisions [book review]

I bought this book [or more precisely received it from CRC Press as a ({prospective} book) review reward] as I was interested in the author’s perspectives on actual decision making (and unaware of the earlier Statistical Decision Theory book he had written in 2013). It is intended for a postgraduate semester course and  “not for a beginner in statistics”. Exercises with solutions are included in each chapter (with some R codes in the solutions). From Chapter 4 onwards, the “Further reading suggestions” are primarily referring to papers and books written by the author, as these chapters are based on his earlier papers.

“I regard hypothesis testing as a distraction from and a barrier to good statistical practice. Its ritualised application should be resisted from the position of strength, by being well acquainted with all its theoretical and practical aspects. I very much hope (…) that the right place for hypothesis testing is in a museum, next to the steam engine.”

The first chapter exposes the shortcomings of hypothesis testing for conducting decision making, in particular by ignoring the consequences of the decisions. A perspective with which I agree, but I fear the subsequent developments found in the book remain too formalised to be appealing, reverting to the over-simplification found in Neyman-Pearson theory. The second chapter is somewhat superfluous for a book assuming a prior exposure to statistics, with a quick exposition of the frequentist, Bayesian, and … fiducial paradigms. With estimators being first defined without referring to a specific loss function. And I find the presentation of the fiducial approach rather shaky (if usual). Esp. when considering fiducial perspective to be used as default Bayes in the subsequent chapters. I also do not understand the notation (p.31)

outside of a Bayesian (or fiducial?) framework. (I did not spot typos aside from the traditional “the the” duplicates, with at least six occurences!)

The aforementioned subsequent chapters are not particularly enticing as they cater to artificial loss functions and engage into detailed derivations that do not seem essential. At times they appear to be nothing more than simple calculus exercises. The very construction of the loss function, which I deem critical to implement statistical decision theory, is mostly bypassed. The overall setting is also frighteningly unidimensional. In the parameter, in the statistic, and in the decision. Covariates only appear in the final chapter which appears to have very little connection with decision making in that the loss function there is the standard quadratic loss, used to achieve the optimal composition of estimators, rather than selecting the best model. The book is also missing in practical or realistic illustrations.

“With a bit of immodesty and a tinge of obsession, I would like to refer to the principal theme of this book as a paradigm, ascribing to it as much importance and distinction as to the frequentist and Bayesian paradigms”

The book concludes with a short postscript (pp.247-249) reproducing the introducing paragraphs about the ill-suited nature of hypothesis testing for decision-making. Which would have been better supported by a stronger engagement into elicitating loss functions and quantifying the consequences of actions from the clients…

[Disclaimer about potential self-plagiarism: this post or an edited version will eventually appear in my Book Review section in CHANCE.]

Introduction to Sequential Monte Carlo [book review]

[Warning: Due to many CoI, from Nicolas being a former PhD student of mine, to his being a current colleague at CREST, to Omiros being co-deputy-editor for Biometrika, this review will not be part of my CHANCE book reviews.]

My friends Nicolas Chopin and Omiros Papaspiliopoulos wrote in 2020 An Introduction to Sequential Monte Carlo (Springer) that took several years to achieve and which I find remarkably coherent in its unified presentation. Particles filters and more broadly sequential Monte Carlo have expended considerably in the last 25 years and I find it difficult to keep track of the main advances given the expansive and heterogeneous literature. The book is also quite careful in its mathematical treatment of the concepts and, while the Feynman-Kac formalism is somewhat scary, it provides a careful introduction to the sampling techniques relating to state-space models and to their asymptotic validation. As an introduction it does not go to the same depths as Pierre Del Moral’s 2004 book or our 2005 book (Cappé et al.). But it also proposes a unified treatment of the most recent developments, including SMC² and ABC-SMC. There is even a chapter on sequential quasi-Monte Carlo, naturally connected to Mathieu Gerber’s and Nicolas Chopin’s 2015 Read Paper. Another significant feature is the articulation of the practical part around a massive Python package called particles [what else?!]. While the book is intended as a textbook, and has been used as such at ENSAE and in other places, there are only a few exercises per chapter and they are not necessarily manageable (as Exercise 7.1, the unique exercise for the very short Chapter 7.) The style is highly pedagogical, take for instance Chapter 10 on the various particle filters, with a detailed and separate analysis of the input, algorithm, and output of each of these. Examples are only strategically used when comparing methods or illustrating convergence. While the MCMC chapter (Chapter 15) is surprisingly small, it is actually an introducing of the massive chapter on particle MCMC (and a teaser for an incoming Papaspiloulos, Roberts and Tweedie, a slow-cooking dish that has now been baking for quite a while!).

Data Science & Machine Learning book free for download

Monte Carlo Markov chains

Darren Wraith pointed out this (currently free access) Springer book by Massimiliano Bonamente [whose family name means good spirit in Italian] to me for its use of the unusual Monte Carlo Markov chain rendering of MCMC.  (Google Trend seems to restrict its use to California!) This is a graduate text for physicists, but one could nonetheless expect more rigour in the processing of the topics. Particularly of the Bayesian topics. Here is a pot-pourri of memorable quotes:

“Two major avenues are available for the assignment of probabilities. One is based on the repetition of the experiments a large number of times under the same conditions, and goes under the name of the frequentist or classical method. The other is based on a more theoretical knowledge of the experiment, but without the experimental requirement, and is referred to as the Bayesian approach.”

“The Bayesian probability is assigned based on a quantitative understanding of the nature of the experiment, and in accord with the Kolmogorov axioms. It is sometimes referred to as empirical probability, in recognition of the fact that sometimes the probability of an event is assigned based upon a practical knowledge of the experiment, although without the classical requirement of repeating the experiment for a large number of times. This method is named after the Rev. Thomas Bayes, who pioneered the development of the theory of probability.”

“The likelihood P(B/A) represents the probability of making the measurement B given that the model A is a correct description of the experiment.”

“…a uniform distribution is normally the logical assumption in the absence of other information.”

“The Gaussian distribution can be considered as a special case of the binomial, when the number of tries is sufficiently large.”

“This clearly does not mean that the Poisson distribution has no variance—in that case, it would not be a random variable!”

“The method of moments therefore returns unbiased estimates for the mean and variance of every distribution in the case of a large number of measurements.”

“The great advantage of the Gibbs sampler is the fact that the acceptance is 100 %, since there is no rejection of candidates for the Markov chain, unlike the case of the Metropolis–Hastings algorithm.”

Let me then point out (or just whine about!) the book using “statistical independence” for plain independence, the use of / rather than Jeffreys’ | for conditioning (and sometimes forgetting \ in some LaTeX formulas), the confusion between events and random variables, esp. when computing the posterior distribution, between models and parameter values, the reliance on discrete probability for continuous settings, as in the Markov chain chapter, confusing density and probability, using Mendel’s pea data without mentioning the unlikely fit to the expected values (or, as put more subtly by Fisher (1936), “the data of most, if not all, of the experiments have been falsified so as to agree closely with Mendel’s expectations”), presenting Fisher’s and Anderson’s Iris data [a motive for rejection when George was JASA editor!] as a “a new classic experiment”, mentioning Pearson but not Lee for the data in the 1903 Biometrika paper “On the laws of inheritance in man” (and woman!), and not accounting for the discrete nature of this data in the linear regression chapter, the three page derivation of the Gaussian distribution from a Taylor expansion of the Binomial pmf obtained by differentiating in the integer argument, spending endless pages on deriving standard properties of classical distributions, this appalling mess of adding over the conditioning atoms with no normalisation in a Poisson experiment

,

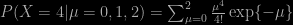botching the proof of the CLT, which is treated before the Law of Large Numbers, restricting maximum likelihood estimation to the Gaussian and Poisson cases and muddling its meaning by discussing unbiasedness, confusing a drifted Poisson random variable with a drift on its parameter, as well as using the pmf of the Poisson to define an area under the curve (Fig. 5.2), sweeping the improperty of a constant prior under the carpet, defining a null hypothesis as a range of values for a summary statistic, no mention of Bayesian perspectives in the hypothesis testing, model comparison, and regression chapters, having one-dimensional case chapters followed by two-dimensional case chapters, reducing model comparison to the use of the Kolmogorov-Smirnov test, processing bootstrap and jackknife in the Monte Carlo chapter without a mention of importance sampling, stating recurrence results without assuming irreducibility, motivating MCMC by the intractability of the evidence, resorting to the term link to designate the current value of a Markov chain, incorporating the need for a prior distribution in a terrible description of the Metropolis-Hastings algorithm, including a discrete proof for its stationarity, spending many pages on early 1990’s MCMC convergence tests rather than discussing the adaptive scaling of proposal distributions, the inclusion of numerical tables [in a 2017 book] and turning Bayes (1763) into Bayes and Price (1763), or Student (1908) into Gosset (1908).

[Usual disclaimer about potential self-plagiarism: this post or an edited version of it could possibly appear later in my Books Review section in CHANCE. Unlikely, though!]