ten computer codes that transformed science

In a “Feature” article of 21 January 2021, Nature goes over a poll on “software tools that have had a big impact on the world of science”. Among those,

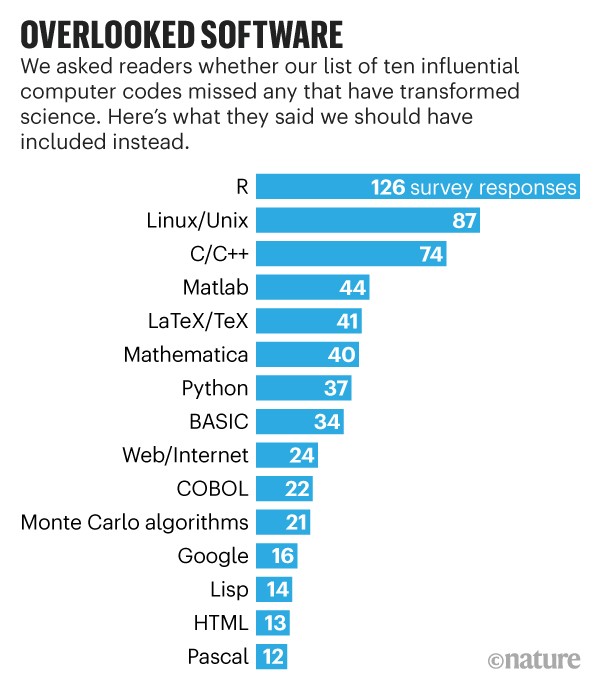
the Fortran compiler (1957), which is one of the first symbolic languages, developed by IBM. This is the first computer language I learned (in 1982) and one of the two (with SAS) I ever coded on punch cards for the massive computers of INSEE. I quickly and enthusiastically switched to Pascal (and the Apple IIe) the year after and despite an attempt at moving to C, I alas kept the Pascal programming style in my subsequent C codes (until I gave up in the early 2000’s!). Moving to R full time, even though I had been using Splus since a Unix version was produced. Interestingly, a later survey of Nature readers put R at the top of the list of what should have been included!, incidentally including Monte Carlo algorithms into the list (and I did not vote in that poll!),

the fast Fourier transform (1965), co-introduced by John Tukey, but which I never ever used (or at least knowingly!),

arXiv (1991), which was started as an emailed preprint list by Paul Ginsparg at Los Alamos, getting the current name by 1998, and where I only started publishing (or arXiving) in 2007, perhaps because it then sounded difficult to submit a preprint there, perhaps because having a worldwide preprint server sounded more like bother (esp. since we had then to publish our preprints on the local servers) than revolution, perhaps because of a vague worry of being overtaken by others… Anyway, I now see arXiv as the primary outlet for publishing papers, with the possible added features of arXiv-backed journals and Peer Community validations,

the IPython Notebook (2011), by Fernando Pérez, which started by 259 lines of Python code, and turned into Jupyter in 2014. I know nothing about this, but I can relate to the relevance of the project when thinking about Rmarkdown, which I find more and more to be a great way to work on collaborative projects and to teach. And for producing reproducible research. (I do remember writing once a paper in Sweave, but not which one…!)

hard birthday problem

Click to access birthday.pdf

From an X validated question, found that WordPress now allows for direct link to pdf documents, like the above paper by my old friend Anirban Das Gupta! The question is about estimating a number M of individuals with N distinct birth dates over a year of T days. After looking around I could not find a simpler representation of the probability for N=r other than (1) in my answer,

borrowed from a paper by Fisher et al. (Another Fisher!) Checking Feller leads to the probability (p.102)

which fits rather nicely simulation frequencies, as shown using

apply(!apply(matrix(sample(1:Nb,T*M,rep=TRUE),T,M),1,duplicated),2,sum)

Further, Feller (1970, pp.103-104) justifies an asymptotic Poisson approximation with parameter$

from which an estimate of $M$ can be derived. With the birthday problem as illustration (pp.105-106)!

It may be that a completion from N to (R¹,R²,…) where the components are the number of days with one birthdate, two birthdates, &tc. could help design an EM algorithm that would remove the summation in (1) but I did not spend more time on the problem (than finding a SAS approximation to the probability!).

Jean-Paul Benzécri (1932-2019)

I learned last weekend that Jean-Paul Benzécri had died earlier in the week. He was a leading and charismatic figure of the French renewal in data analysis (or analyse des données) that used mostly algebraic tools to analyse large datasets, while staying as far as possible from the strong abstraction of French statistics at that time. While I did not know him on a personal basis, I remember from my lecturer years there that he used to come to Institut de Statistique de l’Université de Paris (ISUP), Université Pierre et Marie Curie, once a week and meet with a large group of younger statisticians, students and junior faculty, and then talk to them for long hours while walking back and forth along the corridor in Jussieu. Showing extreme dedication from the group as this windowless corridor was particularly ghastly! (I also remember less fondly hours spent over piles and piles of SAS printout trying to make sense of multiple graphs of projections produced by these algebraic methods and feeling there were too many degrees of freedom for them to feel rigorous enough.)

don’t be late for BayesComp’2020

An important reminder that October 14 is the deadline for regular registration to BayesComp 2020 as late fees will apply afterwards!!! The conference looks attractive enough to agree to pay more, but still…

deadlines for BayesComp’2020

While I have forgotten to send a reminder that August 15 was the first deadline of BayesComp 2020 for the early registrations, here are further deadlines and dates

1. BayesComp 2020 occurs on January 7-10 2020 in Gainesville, Florida, USA
2. Registration is open with regular rates till October 14, 2019
3. Deadline for submission of poster proposals is December 15, 2019
4. Deadline for travel support applications is September 20, 2019
5. There are four free tutorials on January 7, 2020, related with Stan, NIMBLE, SAS, and AutoStat