matrix multiplication [cover]

ten computer codes that transformed science

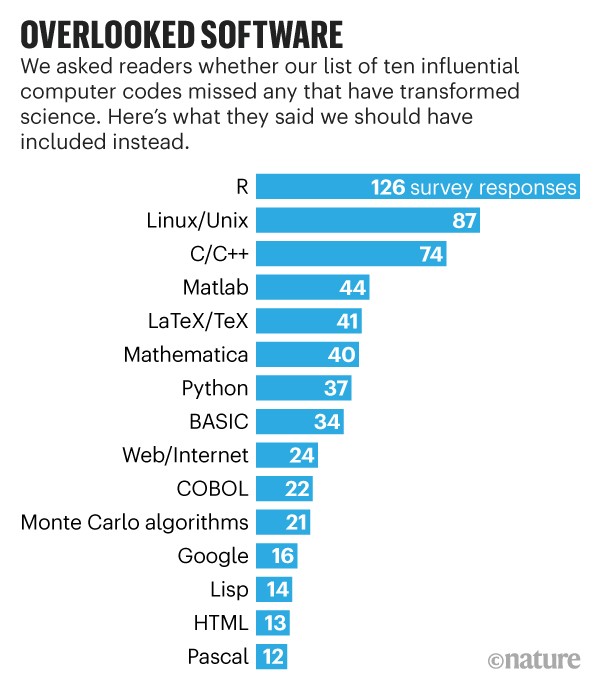In a “Feature” article of 21 January 2021, Nature goes over a poll on “software tools that have had a big impact on the world of science”. Among those,

the Fortran compiler (1957), which is one of the first symbolic languages, developed by IBM. This is the first computer language I learned (in 1982) and one of the two (with SAS) I ever coded on punch cards for the massive computers of INSEE. I quickly and enthusiastically switched to Pascal (and the Apple IIe) the year after and despite an attempt at moving to C, I alas kept the Pascal programming style in my subsequent C codes (until I gave up in the early 2000’s!). Moving to R full time, even though I had been using Splus since a Unix version was produced. Interestingly, a later survey of Nature readers put R at the top of the list of what should have been included!, incidentally including Monte Carlo algorithms into the list (and I did not vote in that poll!),

the fast Fourier transform (1965), co-introduced by John Tukey, but which I never ever used (or at least knowingly!),

arXiv (1991), which was started as an emailed preprint list by Paul Ginsparg at Los Alamos, getting the current name by 1998, and where I only started publishing (or arXiving) in 2007, perhaps because it then sounded difficult to submit a preprint there, perhaps because having a worldwide preprint server sounded more like bother (esp. since we had then to publish our preprints on the local servers) than revolution, perhaps because of a vague worry of being overtaken by others… Anyway, I now see arXiv as the primary outlet for publishing papers, with the possible added features of arXiv-backed journals and Peer Community validations,

the IPython Notebook (2011), by Fernando Pérez, which started by 259 lines of Python code, and turned into Jupyter in 2014. I know nothing about this, but I can relate to the relevance of the project when thinking about Rmarkdown, which I find more and more to be a great way to work on collaborative projects and to teach. And for producing reproducible research. (I do remember writing once a paper in Sweave, but not which one…!)

Berni Alder obituary in Nature [and the Metropolis algorithm]

When reading through the 15 October issue of Nature, I came across an obituary by David Ceperley for Berni Alder (1925-2020). With Thomas Wainwright, Alder invented the technique of molecular dynamics, “silencing criticism that the results were the product of inaccurate computer arithmetic.” 

“Berni Alder pioneered computer simulation, in particular of the dynamics of atoms and molecules in condensed matter. To answer fundamental questions, he encouraged the view that computer simulation was a new way of doing science, one that could connect theory with experiment. Alder’s vision transformed the field of statistical mechanics and many other areas of applied science.”

As I was completely unaware of Alder’s contributions to the field, I was most surprised to read the following

“During his PhD, he and the computer scientist Stan Frankel developed an early Monte Carlo algorithm — one in which the spheres are given random displacements — to calculate the properties of the hard-sphere fluid. The advance was scooped by Nicholas Metropolis and his group at the Los Alamos National Laboratory in New Mexico.”

that would imply missing credit is due!, but I could only find the following information on Stan Frankel’s Wikipedia page: Frankel “worked with PhD candidate Berni Alder in 1949–1950 to develop what is now known as Monte Carlo analysis. They used techniques that Enrico Fermi had pioneered in the 1930s. Due to a lack of local computing resources, Frankel travelled to England in 1950 to run Alder’s project on the Manchester Mark 1 computer. Unfortunately, Alder’s thesis advisor [John Kirkwood] was unimpressed, so Alder and Frankel delayed publication of their results until 1955, in the Journal of Chemical Physics. This left the major credit for the technique to a parallel project by a team including Teller and Metropolis who published similar work in the same journal in 1953.” The (short) paper by Alder, Frankel and Lewinson is however totally silent on a potential precursor to the Metropolis et al. algorithm (included in its references)… It also contains a proposal for a completely uniform filling of a box by particles, provided they do not overlap, but the authors had to stop at 98 particles due to its inefficiency.

infinite mixtures are likely to take a while to simulate

Another question on X validated got me highly interested for a while, as I had considered myself the problem in the past, until I realised while discussing with Murray Pollock in Warwick that there was no general answer: when a density f is represented as an infinite series decomposition into weighted densities, some weights being negative, is there an efficient way to generate from such a density? One natural approach to the question is to look at the mixture with positive weights, f⁺, since it gives an upper bound on the target density. Simulating from this upper bound f⁺ and accepting the outcome x with probability equal to the negative part over the sum of the positive and negative parts f⁻(x)/f(x) is a valid solution. Except that it is not implementable if

1.  the positive and negative parts both involve infinite sums with no exploitable feature that can turn them into finite sums or closed form functions,
2.  the sum of the positive weights is infinite, which is the case when the series of the weights is not absolutely converging.

Even when the method is implementable it may be arbitrarily inefficient in the sense that the probability of acceptance is equal to to the inverse of the sum of the positive weights and that simulating from the bounding mixture in the regular way uses the original weights which may be unrelated in size with the actual importance of the corresponding components in the actual target. Hence, when expressed in this general form, the problem cannot allow for a generic solution.

Obviously, if more is known about the components of the mixture, as for instance the sequence of weights being alternated, there exist specialised methods, as detailed in the section of series representations in Devroye’s (1985) simulation bible. For instance, in the case when positive and negative weight densities can be paired, in the sense that their weighted difference is positive, a latent index variable can be included. But I cannot think of a generic method where the initial positive and negative components are used for simulation, as it may on the opposite be the case that no finite sum difference is everywhere positive.

the three-body problem [book review]

“Back then, I thought of one thing: Have you heard of the Monte Carlo method? Ah, it’s a computer algorithm often used for calculating the area of irregular shapes. Specifically, the software puts the figure of interest in a figure of known area, such as a circle, and randomly strikes it with many tiny balls, never targeting the same spot twice. After a large number of balls, the proportion of balls that fall within the irregular shape compared to the total number of balls used to hit the circle will yield the area of the shape. Of course, the smaller the balls used, the more accurate the result.

Although the method is simple, it shows how, mathematically, random brute force can overcome precise logic. It’s a numerical approach that uses quantity to derive quality. This is my strategy for solving the three-body problem. I study the system moment by moment. At each moment, the spheres’ motion vectors can combine in infinite ways. I treat each combination like a life form. The key is to set up some rules: which combinations of motion vectors are “healthy” and “beneficial,” and which combinations are “detrimental” and “harmful.” The former receive a survival advantage while the latter are disfavored. The computation proceeds by eliminating the disadvantaged and preserving the advantaged. The final combination that survives is the correct prediction for the system’s next configuration, the next moment in time.”

While I had read rather negative reviews of the Three-Body Problem, I still decided to buy the book from an Oxford bookstore and give it a try. Ìf only because this was Chinese science-fiction and I had never read any Chinese science-fiction. (Of course the same motivation would apply for most other countries!) While the historical (or pseudo-historical) part of the novel is most interesting, about the daughter of a university physicist killed by Red Guards during the Cultural Revolution and hence forever suspect, even after decades of exile, the science-fiction part about contacting another inhabited planet and embracing its alien values based on its sole existence is quite deficient and/or very old-fashioned. As is [old-fashioned] the call to more than three dimensions to manage anything, from space travel to instantaneous transfer of information, to ultimate weapons. And an alien civilization that is not dramatically alien. As for the three body problem itself, there is very little of interest in the book and the above quote on using Monte Carlo to “solve” the three-body problem is not of any novelty since it started in the early 1940’s.

I am thus very much surprised at the book getting a Hugo award. For a style that is more reminiscent of early Weird Tales than of current science-fiction… In addition, the characters are rather flat and often act in unnatural ways. (Some critics blame the translation, but I think it gets deeper than that.)